HBLbits_Verilog Basic_Rule90

HBLbits_Verilog Basic_Rule90

Rule 90

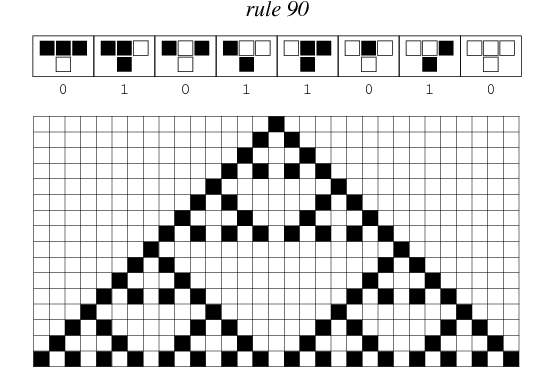
Rule 90 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation . This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).

Starting with a single black cell, successive generations are given by interpreting the numbers 1, 5, 17, 85, 257, 1285, 4369, 21845, ... (OEIS A038183) in binary, namely as 1, 101, 10001, 1010101, 100000001, ... (OEIS A070886).

Rule 90 is amphichiral, and its complement is rule 165.

The fractal produced by this rule was described by Sierpiński in 1915 and appearing in Italian art from the 13th century (Wolfram 2002, p. 43). It is therefore also known as the Sierpiński sieve, Sierpiński gasket, or Sierpiński triangle. The binomial coefficient  mod 2 can be computed using the XOR operation  XOR , making Pascal's triangle mod 2 very easy to construct. Moreover, coloring all odd numbers black and even numbers white in Pascal's triangle produces a Sierpiński sieve (Guy 1990; Wolfram 2002, p. 870).

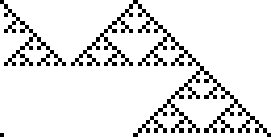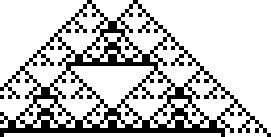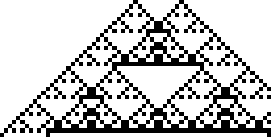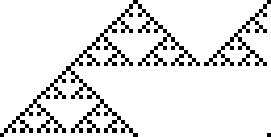
Rule 90 is one of the eight additive elementary cellular automata (Wolfram 2002, p. 952).

In the case of Rule 90, each cell's new value is the exclusive or of the two neighboring values. Equivalently, the next state of this particular automaton is governed by the following rule table:^[1]

current pattern	111	110	101	100	011	010	001	000
new state for center cell	0	1	0	1	1	0	1	0

Binary 01011010 = 90

Rule 90 is a one-dimensional cellular automaton with interesting properties.

The rules are simple. There is a one-dimensional array of cells (on or off). At each time step, the next state of each cell is the XOR of the cell's two current neighbours. A more verbose way of expressing this rule is the following table, where a cell's next state is a function of itself and its two neighbours:

Left	Center	Right	Center's next state
1	1	1	0
1	1	0	1
1	0	1	0
1	0	0	1
0	1	1	1
0	1	0	0
0	0	1	1
0	0	0	0

(The name "Rule 90" comes from reading the "next state" column: 01011010 is decimal 90.)

In this circuit, create a 512-cell system (q[511:0]), and advance by one time step each clock cycle. The load input indicates the state of the system should be loaded with data[511:0]. Assume the boundaries (q[-1] and q[512]) are both zero (off).

module top_module(

    input clk,

    input load,

    input [511:0] data,

    output [511:0] q ); 

always @(posedge clk) begin

if (load)

q <= data; // Load the DFFs with a value.

else begin

            // At each clock, the DFF storing each bit position becomes the XOR of its left neighbour

// and its right neighbour. Since the operation is the same for every

// bit position, it can be written as a single operation on vectors.

// The shifts are accomplished using part select and concatenation operators.

//   left           right

//  neighbour       neighbour

            q <= {1'b0,q[511:1]} ^ {q[510:0], 1'b0} ;

end

end

endmodule