HBLbits_Verilog Basic_Conwaylife

 HBLbits_Verilog Basic_Conwaylife

康威生命遊戲（英語：Conway's Game of Life），又稱康威生命棋，是英國數學家約翰·何頓·康威在1970年發明的細胞自動機。

它最初於1970年10月在《科學美國人》雜誌上馬丁·葛登能的「數學遊戲」專欄出現。

康威生命遊戲中的一種可持續繁殖模式：「高斯帕機槍」不斷製造「滑翔機」

康威生命遊戲中的較複雜演化模式：「播種機」模式不斷生成「高斯帕機槍」來製造「滑翔機」

生命遊戲中，對於任意細胞，規則如下：

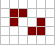
• 每個細胞有兩種狀態 - 存活或死亡，每個細胞與以自身為中心的周圍八格細胞產生互動（如圖，黑色為存活，白色為死亡）
• 當前細胞為存活狀態時，當周圍的存活細胞低於2個時（不包含2個），該細胞變成死亡狀態。（模擬生命數量稀少）
• 當前細胞為存活狀態時，當周圍有2個或3個存活細胞時，該細胞保持原樣。
• 當前細胞為存活狀態時，當周圍有超過3個存活細胞時，該細胞變成死亡狀態。（模擬生命數量過多）
• 當前細胞為死亡狀態時，當周圍有3個存活細胞時，該細胞變成存活狀態。（模擬繁殖）

可以把最初的細胞結構定義為種子，當所有在種子中的細胞同時被以上規則處理後，可以得到第一代細胞圖。按規則繼續處理當前的細胞圖，可以得到下一代的細胞圖，周而復始。

概述[編輯]

生命遊戲是一個零玩家遊戲。它包括一個二維矩形世界，這個世界中的每個方格居住著一個活著的或死了的細胞。一個細胞在下一個時刻生死取決於相鄰八個方格中活著的或死了的細胞的數量。如果相鄰方格活著的細胞數量過多，這個細胞會因為資源匱乏而在下一個時刻死去；相反，如果周圍活細胞過少，這個細胞會因太孤單而死去。實際中，玩家可以設定周圍活細胞的數目怎樣時才適宜該細胞的生存。如果這個數目設定過高，世界中的大部分細胞會因為找不到太多的活的鄰居而死去，直到整個世界都沒有生命；如果這個數目設定過低，世界中又會被生命充滿而沒有什麼變化。

實際中，這個數目一般選取2或者3；這樣整個生命世界才不至於太過荒涼或擁擠，而是一種動態的平衡。這樣的話，遊戲的規則就是：當一個方格周圍有2或3個活細胞時，方格中的活細胞在下一個時刻繼續存活；即使這個時刻方格中沒有活細胞，在下一個時刻也會「誕生」活細胞。

在這個遊戲中，還可以設定一些更加複雜的規則，例如當前方格的狀況不僅由父一代決定，而且還考慮祖父一代的情況。玩家還可以作為這個世界的「上帝」，隨意設定某個方格細胞的死活，以觀察對世界的影響。

在遊戲的進行中，雜亂無序的細胞會逐漸演化出各種精緻、有形的結構；這些結構往往有很好的對稱性，而且每一代都在變化形狀。一些形狀已經鎖定，不會逐代變化。有時，一些已經成形的結構會因為一些無序細胞的「入侵」而被破壞。但是形狀和秩序經常能從雜亂中產生出來。

這個遊戲被許多電腦程式實現了。Unix世界中的許多駭客喜歡玩這個遊戲，他們用字符代表一個細胞，在一個計算機屏幕上進行演化。比較著名的例子是，GNU Emacs編輯器中就包括這樣一個小遊戲。

生命遊戲是一個零玩家遊戲。它包括一個二維矩形世界，這個世界中的每個方格居住著一個活著的或死了的細胞。一個細胞在下一個時刻生死取決於相鄰八個方格中活著的或死了的細胞的數量。如果相鄰方格活著的細胞數量過多，這個細胞會因為資源匱乏而在下一個時刻死去；相反，如果周圍活細胞過少，這個細胞會因太孤單而死去。實際中，玩家可以設定周圍活細胞的數目怎樣時才適宜該細胞的生存。如果這個數目設定過高，世界中的大部分細胞會因為找不到太多的活的鄰居而死去，直到整個世界都沒有生命；如果這個數目設定過低，世界中又會被生命充滿而沒有什麼變化。

實際中，這個數目一般選取2或者3；這樣整個生命世界才不至於太過荒涼或擁擠，而是一種動態的平衡。這樣的話，遊戲的規則就是：當一個方格周圍有2或3個活細胞時，方格中的活細胞在下一個時刻繼續存活；即使這個時刻方格中沒有活細胞，在下一個時刻也會「誕生」活細胞。

在這個遊戲中，還可以設定一些更加複雜的規則，例如當前方格的狀況不僅由父一代決定，而且還考慮祖父一代的情況。玩家還可以作為這個世界的「上帝」，隨意設定某個方格細胞的死活，以觀察對世界的影響。

在遊戲的進行中，雜亂無序的細胞會逐漸演化出各種精緻、有形的結構；這些結構往往有很好的對稱性，而且每一代都在變化形狀。一些形狀已經鎖定，不會逐代變化。有時，一些已經成形的結構會因為一些無序細胞的「入侵」而被破壞。但是形狀和秩序經常能從雜亂中產生出來。

這個遊戲被許多電腦程式實現了。Unix世界中的許多駭客喜歡玩這個遊戲，他們用字符代表一個細胞，在一個計算機屏幕上進行演化。比較著名的例子是，GNU Emacs編輯器中就包括這樣一個小遊戲。

穩定狀態[編輯]

• 

  板凳

 
• 

  麵包

 
• 

  蜂巢

 
• 

  大船

 
• 

  小船

 
• 

  花

 
• 

  池塘

 
• 

  蛇

 
• 

  航空母艦

 
• 

  獨木舟

 
• 

  芒果

 
• 

  鴨子

The "game" is played on a two-dimensional grid of cells, where each cell is either 1 (alive) or 0 (dead). At each time step, each cell changes state depending on how many neighbours it has:

• 0-1 neighbour: Cell becomes 0.
• 2 neighbours: Cell state does not change.
• 3 neighbours: Cell becomes 1.
• 4+ neighbours: Cell becomes 0.

The game is formulated for an infinite grid. In this circuit, we will use a 16x16 grid. To make things more interesting, we will use a 16x16 toroid, where the sides wrap around to the other side of the grid. For example, the corner cell (0,0) has 8 neighbours: (15,1), (15,0), (15,15), (0,1), (0,15), (1,1), (1,0), and (1,15). The 16x16 grid is represented by a length 256 vector, where each row of 16 cells is represented by a sub-vector: q[15:0] is row 0, q[31:16] is row 1, etc. (This tool accepts SystemVerilog, so you may use 2D vectors if you wish.)

• load: Loads data into q at the next clock edge, for loading initial state.
• q: The 16x16 current state of the game, updated every clock cycle.

The game state should advance by one timestep every clock cycle.

John Conway, mathematician and creator of the Game of Life cellular automaton, passed away from COVID-19 on April 11, 2020.