常微分程求解:Runge-Kutta 隆巨—庫塔法、高階方法的圖像
源自於http://boson4.phys.tku.edu.tw/numerical_methods/nm_units/ODE_Runge-Kutta.htm
演算法公式與其圖像表示
Euler Mehod
對於一個微小的步幅 (step) h 而言, 若從第 n 步要推到第 n+1 的方法是依以下的方式,就是前面已經提到過的奧依勒法:
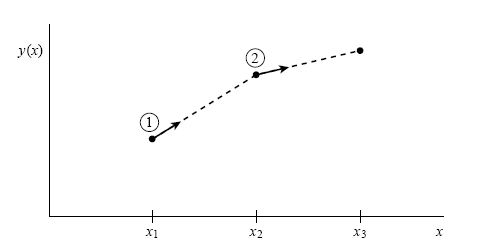
從圖像上來看,它是以第 n 點為立足點,在那裏求出切線方向出發(斜率函數是題目給的),利用該方向來走一步,到達第 n+1 點,如此一步一步地走下去,如下圖所示:
2nd Order Runge-Kutta Method
前面我給大家示範過,利用兩個半步與一個整步的組合,可以創造出精確度達到二階(即誤差從三階開始),但卻只要乘上微小量 h 一次的公式的公式,其中必須付出的代價是,比起上面的 Euler 法要多算 k2(請注意到它是求值在半步的地方):
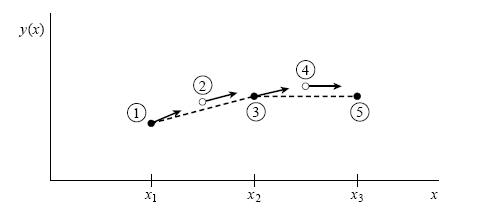
上面的公式從圖像上很容易可以看出其策略,在起點處所求得的斜率,先只走一半到中間點,在那裏再求一次斜率,然後退回到起點利用這個中點斜率走完整一步到下一步,如此得到 yn+1,就是圖上標為 (3) 的地方。這就是一個二階的 step,下一個 step 會落在標為 (5) 處,如此再一次一次走下去。 整個策略看起來,有進兩步、退一步,以退為進的感覺。
4th Order Runge-Kutta Method
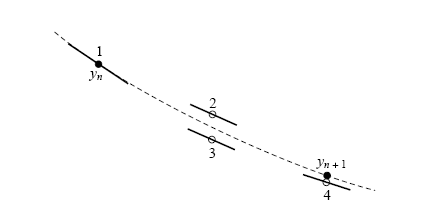
最常用且通用的 RK 方法是四階的,我們可以想見它是由更多不同樣式的半步組合所構成,其中並包含了原有的起點處定斜率與終點處定斜率,請注意這裏 k1、k2、k3、k4 的定義與其相依性(即 k4 用到 k3、k3 用到 k2、k2 用到 k1 的狀況)
(事實上)這裏的圖是有印錯的情況,我認為 2 與 3 的標注處應該對調,公式中的 k1、k2、k3、k4 全部都有 h ,但分別是乘以 (a) 在起點處 1 求的斜率、(b) 以起點斜率走半步到 2 處求斜率、(c) 一樣從起點開始但,改採前面的半步處 2 之斜率,重走半步到 3 後求斜率,以及最後 (d) 採用上一個於 3 處所獲得的斜率,從起點出發走一整步到 4 處求斜率。
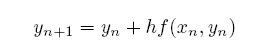
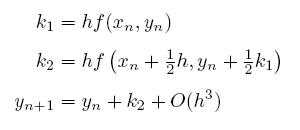
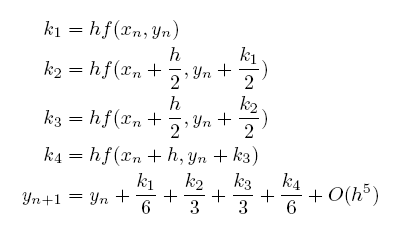


沒有留言:
張貼留言