令  為一個
為一個 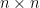 階矩陣。LU 分解是指將
階矩陣。LU 分解是指將  表示為兩個
表示為兩個 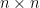 階三角矩陣的乘積
階三角矩陣的乘積
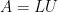 ,
,
其中  是下三角矩陣,
是下三角矩陣,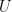 是上三角矩陣,如下例,
是上三角矩陣,如下例,
![\left[\!\!\begin{array}{rrc} 3&-1&2\\ 6&-1&5\\ -9&7&3 \end{array}\!\!\right]=\left[\!\!\begin{array}{rcc} 1&0&0\\ 2&1&0\\ -3&4&1 \end{array}\!\!\right]\left[\!\!\begin{array}{crc} 3&-1&2\\ 0&1&1\\ 0&0&5 \end{array}\!\!\right] \left[\!\!\begin{array}{rrc} 3&-1&2\\ 6&-1&5\\ -9&7&3 \end{array}\!\!\right]=\left[\!\!\begin{array}{rcc} 1&0&0\\ 2&1&0\\ -3&4&1 \end{array}\!\!\right]\left[\!\!\begin{array}{crc} 3&-1&2\\ 0&1&1\\ 0&0&5 \end{array}\!\!\right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Brrc%7D++3%26-1%262%5C%5C++6%26-1%265%5C%5C++-9%267%263++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Brcc%7D++++1%260%260%5C%5C++2%261%260%5C%5C++-3%264%261++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcrc%7D++3%26-1%262%5C%5C++0%261%261%5C%5C++0%260%265++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0) 。
。
LU 分解的本質是高斯消去法的一種表達形式,矩陣  記錄消去法化簡
記錄消去法化簡  的過程,而矩陣
的過程,而矩陣 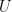 則儲存化簡結果 (見“高斯消去法”)。LU 分解的外表看似平淡無奇,但它可以用來解線性方程,逆矩陣和計算行列式,堪稱是最具實用價值的矩陣分解式之一。
則儲存化簡結果 (見“高斯消去法”)。LU 分解的外表看似平淡無奇,但它可以用來解線性方程,逆矩陣和計算行列式,堪稱是最具實用價值的矩陣分解式之一。
源自於 http://www.gregthatcher.com/Mathematics/LU_Factorization.aspx
This Calculator will Factorize a Square Matrix into the form A=LU where L is a lower triangular matrix, and U is an upper triangular matrix.
Add (2/3 * row1) to row2
(the
elementary matrix, hilighted in yellow, performs this operation for us.)
Add (-1/2 * row1) to row3
(the
elementary matrix, hilighted in yellow, performs this operation for us.)
Add (3/8 * row2) to row3
(the
elementary matrix, hilighted in yellow, performs this operation for us.)
Let's
multiply both sides of the equation by this
inverse.
We can simplify this to:
Let's
multiply both sides of the equation by this
inverse.
We can simplify this to:
Let's
multiply both sides of the equation by this
inverse.
We can simplify this to:
and we have now factored the matrix into the form A=LU.
Note that the 'L' matrix shows us the operations we performed to reduce the matrix (with signs changed).
 為一個
為一個 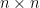 階矩陣。LU 分解是指將
階矩陣。LU 分解是指將  表示為兩個
表示為兩個 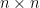 階三角矩陣的乘積
階三角矩陣的乘積 是下三角矩陣,
是下三角矩陣,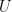 是上三角矩陣,如下例,
是上三角矩陣,如下例, 記錄消去法化簡
記錄消去法化簡  的過程,而矩陣
的過程,而矩陣 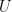 則儲存化簡結果 (見“高斯消去法”)。LU 分解的外表看似平淡無奇,但它可以用來解線性方程,逆矩陣和計算行列式,堪稱是最具實用價值的矩陣分解式之一。
則儲存化簡結果 (見“高斯消去法”)。LU 分解的外表看似平淡無奇,但它可以用來解線性方程,逆矩陣和計算行列式,堪稱是最具實用價值的矩陣分解式之一。

沒有留言:
張貼留言