https://ccjou.wordpress.com/2013/02/22/%E9%AB%98%E6%96%AF%E2%94%80%E7%B4%84%E7%95%B6%E6%B3%95/
高斯─約當法
在解線性方程組的應用上,高斯─約當法[1] (Gauss-Jordan method) 是高斯消去法的延伸 (見“高斯消去法”),其目的要得到最簡約的列等價方程組。高斯消去法產生梯形矩陣後,我們可以繼續執行取代運算將軸元 (pivot) 上方的元悉數消去,並使用伸縮運算迫使軸元為 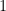 。高斯─約當法產生的矩陣稱為簡約列梯形式 (reduced row echelon form),由下列四個條件定義 (前兩個條件即為梯形矩陣的性質):
。高斯─約當法產生的矩陣稱為簡約列梯形式 (reduced row echelon form),由下列四個條件定義 (前兩個條件即為梯形矩陣的性質):
- 零列置於矩陣最底下。
- 每列軸元的位置都位於其上方各列軸元的右側。
- 軸元等於
。
- 軸元其上方與下方的元皆為零。
下面列舉兩個簡約列梯形式。數字 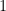 表示軸元,每一軸元上方和下方的元皆為零,其他各元 (以
表示軸元,每一軸元上方和下方的元皆為零,其他各元 (以  表示) 可以是任意數:
表示) 可以是任意數:
我們用一個例子說明高斯─約當法的計算過程。先使用高斯消去法將給定的增廣矩陣 (代表線性方程組) 化簡至梯形矩陣 (運算細節省略):
接著繼續對梯形矩陣執行基本列運算。以伸縮運算使最底下的軸元為 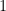 ,再消去該軸元以上的所有元,沿用此方式由下而上直到產生簡約列梯形式,如下:
,再消去該軸元以上的所有元,沿用此方式由下而上直到產生簡約列梯形式,如下:
與高斯消去法得到的梯形矩陣比較,簡約列梯形式的主要價值在於不需要使用反向代入法,當下便可決定線性方程組的解。上例中,從簡約列梯形式具有完整的零列可斷定此方程組是一致的,第一、二、四行為軸行,故
令  ,移項後立刻得到通解
,移項後立刻得到通解

Wilhelm Jordan (1842-1899) From http://upload.wikimedia.org/wikipedia/commons/7/70/Wilhelm_Jordan.png
對於任意給定矩陣,雖然存在許多不同的列等價梯形矩陣,但是萬法歸一,不論基本列運算的執行方式或次序為何,簡約列梯形式總是唯一的,這是因為簡約列梯形式與方程組的解具有一對一的關係 (證明見“簡約列梯形式的唯一性”)。就這層意義來說,列等價的簡約列梯形式是一種典型的矩陣形式。提醒讀者,如果我們的問題僅須解線性方程組,在一般情況下,使用高斯消去法再以反向代入求解的計算效率略優於高斯—約當法直接得到簡約列梯形式。雖然如此,高斯—約當法自有一個特別的應用──計算一個
令
若  是可逆的,則
是可逆的,則 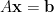 恆有唯一解,基本列運算最終可將增廣矩陣化簡為
恆有唯一解,基本列運算最終可將增廣矩陣化簡為
線性方程組 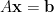 的解即為最右行,
的解即為最右行, ,
, 。若
。若  的簡約列梯形式不等於單位矩陣
的簡約列梯形式不等於單位矩陣 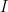 ,便可判定
,便可判定  是不可逆的。令
是不可逆的。令 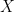 為
為 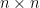 階矩陣使得
階矩陣使得  ,也就是說,
,也就是說,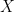 是
是  的逆矩陣
的逆矩陣 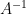 。將
。將 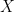 和
和 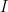 以行向量表示:
以行向量表示: 且
且  ,其中
,其中  代表第
代表第 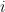 元等於
元等於 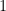 的單位向量,則有
的單位向量,則有
因此,矩陣方程  可分解成
可分解成  個線性方程
個線性方程  。分別對
。分別對  個增廣矩陣
個增廣矩陣  執行高斯─約當法,可得
執行高斯─約當法,可得
但因為這  個增廣矩陣
個增廣矩陣  擁有相同的係數矩陣
擁有相同的係數矩陣  ,我們可以將它們合併成一個大增廣矩陣
,我們可以將它們合併成一個大增廣矩陣 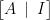 。直接以高斯─約當法化簡大增廣矩陣,即得
。直接以高斯─約當法化簡大增廣矩陣,即得
最後舉一例展示高斯—約當法於計算逆矩陣的應用。考慮
高斯─約當法計算逆矩陣 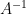 的過程如下:
的過程如下:
從最後一個矩陣可以判斷  是可逆的,
是可逆的,
註解
[1] 高斯─約當法的約當常被人誤認為是法國數學家 Marie Ennemond Camille Jordan(1838-1922),矩陣分析理論中 Jordan 典型形式即因他而名。事實上,高斯─約當法是由德國測地學家 Wihelm Jordan (1842-1899) 於公元1888年提出。



沒有留言:
張貼留言