牛頓法以圖形概念主要是不停在取切線斜率。
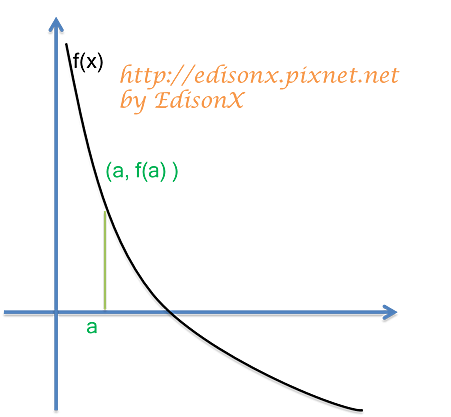
考慮一方程式 f(x) ,一開始必須找到初始點 a,然後代入 f(a)。
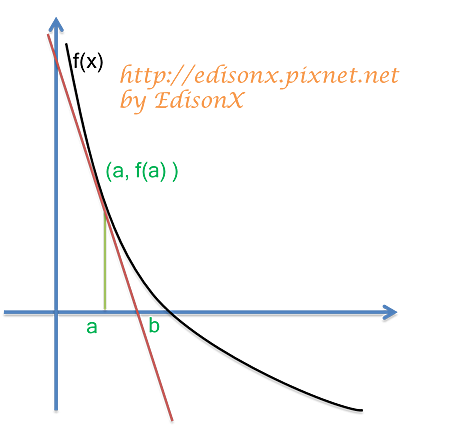
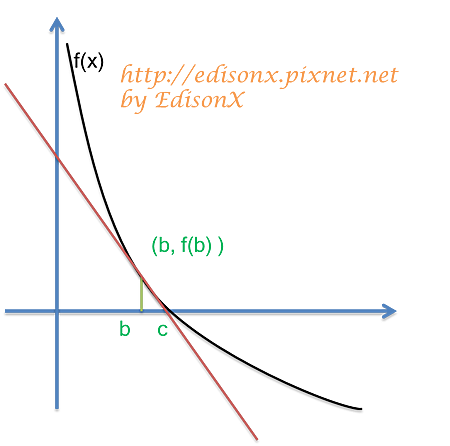
在 f(x) 圖形上,對 (a, f(a)) 做切線,與 x 軸相交於 b 點,且該切線斜率為 f'(a),
連接 (a, f(a) ), (b, 0) 二點,又已知斜率為 f'(a),可得一恆等式
f'(a) = ( 0 - f(a) ) / (b-a)
整理移項,得 b = a - f'(a) / f(a)
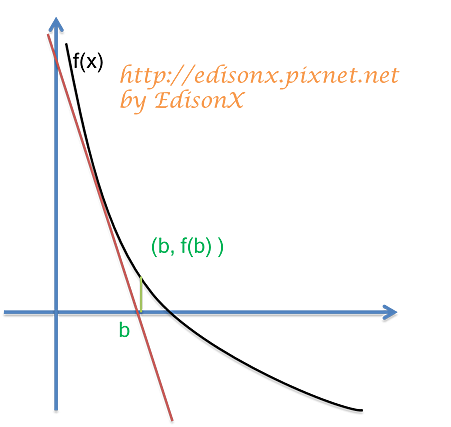
接著再將 b 對應到 f(b) 上去,得到點 (b, f(b))
對 (b, f(b)) 再做切線,切線於 x 軸於 c
有了 (b, f(b)), (c, 0) 兩點,斜率 f'(b),可得切線方程式
c = b - f(b) / f'(b)
再重覆上述動作。若將 a 視為 x0, b 視為 x1, c 視為 x2,
兩個直線公式便成為
x1 = x0 - f(x0) / f'(x0)
x2 = x1 - f(x1) / f'(x1)
依此類推
xk+1 = xk - f(xk) / f'(xk)
一直迭代到 | xk-xk+1 | < eps 或 | f(xk) | < eps 為止。
使用條件與特性
1. 函數 f(x) 必須可微分。
2. 有幾種圖形沒辦法順利收斂,下圖即為其中一種。
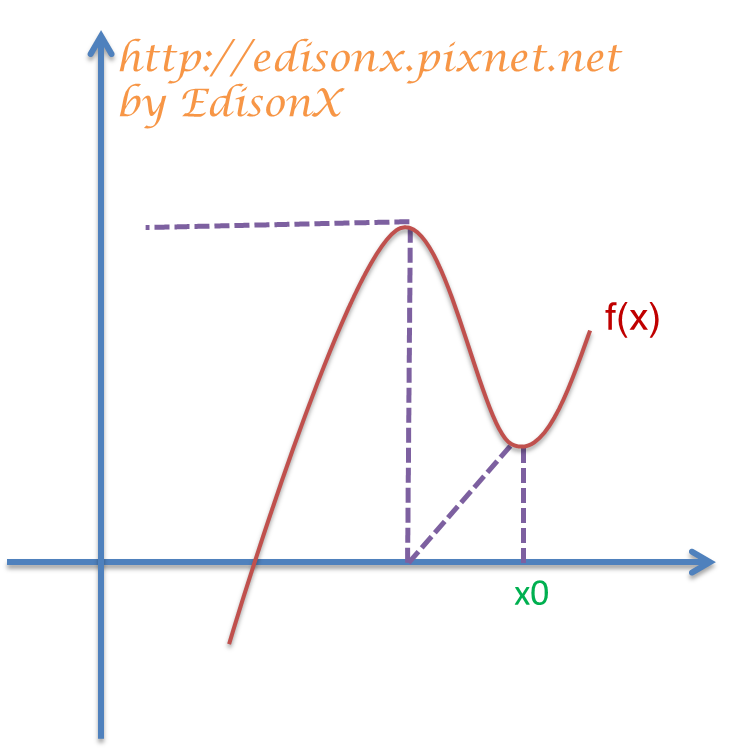
3. 若收斂點為重根,則收斂速度慢,假設已知為 m 個重根,
可將迭代公式改成 xk+1 = xk - m * f(xk) / f'(xk) 。
缺點是,若重根數愈多,則找到的解誤差愈大。
但若未知重根數時,就變得麻煩了,
先設一函式 u(x) = f(x) / f'(x),迭代公式改成
xk+1 = xk - u(xk) / u'(xk),
實作上顯得較為麻煩。
虛擬碼
Algorithm NewtonRoot
E0 : 初始化最小誤差 EPS,初始點 xo
E1 : x = x0
E2 : x0 = x - f(x) / f'(x)
E3 : if abs(x-x0) < eps,演算法結束,傳回 x
E4 : goto E1
End Algorithm
程式碼
/*----------------------------------------------------------------*\
| E0 : 初始化最小誤差EPS,初始點x0
| E1 : x = x0
| E2 : x0 = x - f(x) / f'(x)
| E3 : if abs(x-x0) < eps,演算法結束,傳回x0
| E4 : goto E1
\*----------------------------------------------------------------*/
#include <stdio.h>
#include <math.h>
// [ -2.00 , -1.00 ] , [ 2.00 , 3.00 ] , [ +4.00 , +5.00 ]
double func(double x)
{
double x2=x*x, x3=x2*x;
return (x3 + 4*x2 -10);
}
// funcd(x) = func'(x)
double funcd(double x)
{
double x2=x*x;
return (3*x2 + 8*x);
}
// -------------------------------------------------------
double NewtonRoot(double x0, /* 初點 */
double (*fx)(double), /* 適應函式*/
double (*fd)(double), /* 微分函式*/
double eps, /* 容許誤差*/
int max_itera) /* 最大迭代*/
{
double x=x0;
do{
x0=x;
x = x0 - fx(x0) / fd(x0);
}while(fabs(x-x0)>eps);
return x;
}
int main()
{
const double eps=1E-9;
const int max_iterator=100;
double x0, x;
x0 = -2.0;
x = NewtonRoot(x0, func, funcd, eps, max_iterator);
printf("\n> func(%+.15e) = %+.15e", x, func(x));
x0 = 2.0;
x = NewtonRoot(x0, func, funcd, eps, max_iterator);
printf("\n> func(%+.15e) = %+.15e", x, func(x));
x0 = 4.0 ;
x = NewtonRoot(x0, func, funcd, eps, max_iterator);
printf("\n> func(%+.15e) = %+.15e", x, func(x));
x0 = -10.0 ; // test
x = NewtonRoot(x0, func, funcd, eps, max_iterator);
printf("\n> func(%+.15e) = %+.15e", x, func(x));
return 0;
}
輸出結果
> func(-nan) = -nan
> func(+1.365230013414097e+00) = +0.000000000000000e+00
> func(+1.365230013414097e+00) = +0.000000000000000e+00
> func(+1.365230013414097e+00) = +0.000000000000000e+00
...Program finished with exit code 0
Press ENTER to exit console.
源自於
http://edisonx.pixnet.net/blog/post/35763002-%5Bc%E8%AA%9E%E8%A8%80%E6%95%B8%E5%80%BC%E5%88%86%E6%9E%90%5D-%E9%9D%9E%E7%B7%9A%E6%80%A7%E6%96%B9%E7%A8%8B%E5%BC%8F%E6%B1%82%E8%A7%A3---%E7%89%9B%E9%A0%93%E6%B3%95-n


沒有留言:
張貼留言