穩態熱傳導的問題
源自於https://bime-matlab.blogspot.com/2006/11/1025.html
熱傳導是溫差產生的熱能流動,其流動速率與材料之熱阻係數有關。其公式如下:
q = Q/t
= k A (Th-Tc)/d
= ΔT/(d/kA)
= Δ/R
其中d為材料之厚度,A為截面積,k為熱導係數,其單位為W/[mK]。R則為熱阻,等於d/kA。熱阻的觀念可以用來模擬電路,並進行解析。圖為一道牆由木板、玻璃纖維、水泥及磚牆等材料。這些材質之熱導係數可參閱此網站http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatcond.html#c1。其他相關值如下:
| 材質名稱 | 熱導係數W/[mK] |
|---|---|
| 磚牆 | 0.6 |
| 木材 | 0.12-0.04 |
| 石膏 | 0.08 |
| 玻璃纖維 | 0.04 |
| 玻璃 | 0.8 |
| 水泥 | 0.8 |
| 鐵板 | 50.2 |
| 水 | 0.6 |
將各層產生之熱阻,以電路的方式進行串聯,即可形成類似網路,並計算各層之溫度。其各層間之關係式如下:

以矩陣表示,即為[A][T]=[C]。其溫度T可解如後:
[T]=[A]\[C]
程式說明
程式heat_wall.m可以執行上述之操作。輸入項包括內外溫度(ti,to)、各層熱導係數(k)、厚度(thick)及截面積(area)等。執行後即可得到溫度分佈及熱流(q)等。
程式內容
function [T,x,q]=heat_wall(ti,to,k,thick,area)
% Prog calculating heat transfer through a wall.
% Inputs:
% ti,to: inside & outside temperature, C
% k: thermoconductivities of each layer, W[m.C]
% thick:thickness of each layer, mm
% area:the crosssection area, m^2
% Outputs:
% temp:[heatflow & temperatures at each layer, W/m^2,C
% Example:
% [T,x,q]=heat_wall(20,-10,[0.08 0.04 0.12 0.6],...
% [10 125 60 50])
% Designed by D.S. Fon. Date: Nov. 26, 2006
if nargin<5, area=1;end
R=thick./k/area/1000;
nn=length(thick);C=zeros(1,nn);
CC=-eye(nn)+[[zeros(nn-1,1) eye(nn-1)];C];
A=[R',CC(:,2:end)]
C=[ti C(2:end-1) -to]';
x=[0 cumsum(thick)];
TT=A\C;q=TT(1);T=[ti TT(2:end)' to];
line(x,T,'marker','s')
xlabel('distance,mm')
ylabel('Temperature,C')
執行例:
>> [T,x,q]=heat_wall(25,-10,[0.08 0.04 0.12 0.6], [10 125 60 50])
A =
0.1250 1.0000 0 0
3.1250 -1.0000 1.0000 0
0.5000 0 -1.0000 1.0000
0.0833 0 0 -1.0000
T =
25.0000 23.8587 -4.6739 -9.2391 -10.0000
x =
0 10 135 195 245
q =
9.1304
設室內溫度為攝氏25度,室外為-10度。牆壁由內而外為木板(50mm)、玻璃纖維(100mm)、水泥面(20mm)、磚牆(200mm),其對應之熱導係數分別為[0.12 0.04 0.8 0.6]。以此代入heat_wall程式中執行,得其結果:
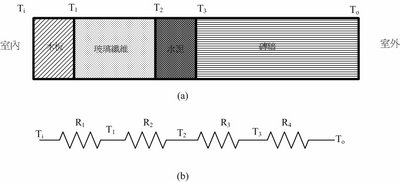 熱阻與電阻之類比關係
熱阻與電阻之類比關係



沒有留言:
張貼留言