C++語言 Simpson’s 1/3 Rule 定積分

Example:

Approximate the value of the integral given below, taking n = 8.

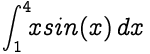
Implementation of Simpson’s 1/3 Rule in C++ is as follows :

#include<iostream>
#include<cmath>
using namespace std;

float f(float x)
{
 return x*sin(x); //Define the function f(x)
}

float simpson(float a, float b, int n)
{
 float h, x[n+1], sum = 0;
 int j;
 h = (b-a)/n;
 
 x[0] = a;
 
 for(j=1; j<=n; j++)
 {
  x[j] = a + h*j;
 }
 
 for(j=1; j<=n/2; j++)
 {
  sum += f(x[2*j - 2]) + 4*f(x[2*j - 1]) + f(x[2*j]);
 }
 
 return sum*h/3;
}

int main()
{
 float a,b,n;
 a = 1;  //Enter lower limit a
 b = 4;  //Enter upper limit b
 n = 8;  //Enter step-length n
 if (n%2 == 0)
  cout<<simpson(a,b,n)<<endl;
 else
  cout<<"n should be an even number";
 return 0;
}