4th Order Runge-Kutta Method
源自
http://boson4.phys.tku.edu.tw/numerical_methods/nm_units/ODE_Runge-Kutta.htm
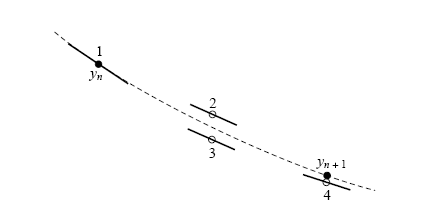
最常用且通用的 RK 方法是四階的,我們可以想見它是由更多不同樣式的半步組合所構成,其中並包含了原有的起點處定斜率與終點處定斜率,請注意這裏 k1、k2、k3、k4 的定義與其相依性(即 k4 用到 k3、k3 用到 k2、k2 用到 k1 的狀況)
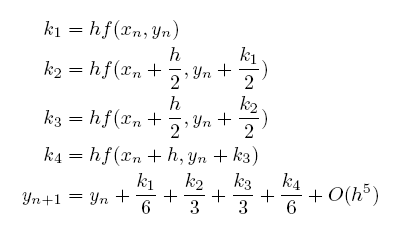
#include<stdio.h>
#include<math.h>
float f(float x,float y);
int main()
{
float x0,y0,m1,m2,m3,m4,m,y,x,h,xn;
x0=0.0;
y0=2.0;
xn=2.0;
h=0.5;
printf("x0=%1.1lf ,y0=%1.1lf ,xn=%1.1lf ,h=%1.1lf",x0,y0,xn,h);
x=x0;
y=y0;
printf("\n\nX\t\t Y\n");
printf("======================\n");
while(x<xn)
{
m1=f(x0,y0);
m2=f((x0+h/2.0),(y0+m1*h/2.0));
m3=f((x0+h/2.0),(y0+m2*h/2.0));
m4=f((x0+h),(y0+m3*h));
m=((m1+2*m2+2*m3+m4)/6);
y=y+m*h;
x=x+h;
printf("%f\t%f\n",x,y);
}
}
float f(float x,float y)
{
float m;
m=(x-y)/(x+y);
return m;
}
輸出畫面
x0=0.0 ,y0=2.0 ,xn=2.0 ,h=0.5
X Y
======================
0.500000 1.621356
1.000000 1.242713
1.500000 0.864069
2.000000 0.485426


沒有留言:
張貼留言