C語言 例題5-11 剛性微分方程 y'(t)=-15y(t) , 0<=t , y(0)=1
真實解 y(t)= exp(-15t)
在數學領域中,剛性方程(stiffness equation)是指一個微分方程,其數值分析的解只有在時間間隔很小時才會穩定,只要時間間隔略大,其解就會不穩定。目前很難去精確地去定義哪些微分方程是剛性方程,然而粗略而言,若此方程式中包含使其快速變動的項,則其為剛性方程。
/* ex5-11.c based on Four-Order Runge-Kutta
* Method to approximate the solution of the
* initial-value problem
* y'=f(y,t), a<=t<=b, y(a)=y0
* at (n+1) equally spaced numbers in the interval
* [a,b]: input a,b,n,and initial condition y0.
*/
// y'(t)=-15y(t) , 0<=t , y(0)=1
// 真實解 y(t)= exp(-15t)
#include <stdio.h>
#include <math.h>
#define F(y,t) (-15*y)
#define W(t) (exp(-15*t))
void main()
{
int i,n=1000;
double a=0.0,b=1.0,y0=1.0,k1,k2,k3,k4,h,t,y,err;
h=(b-a)/n;
t=a;
y=y0;
err=fabs(y-W(t));
printf("t y(t) w(t) error\n");
printf("=====================================\n");
printf("%.2lf %10.7lf %10.7lf %10.7lf\n"
,t,y,W(t),err);
for(i=1;i<=n;i++)
{
k1=h*F(y,t);
k2=h*F((y+k1/2.0),(t+h/2.0));
k3=h*F((y+k2/2.0),(t+h/2.0));
k4=h*F((y+k3),(t+h));
y=y+(k1+2*k2+2*k3+k4)/6.0;
t=a+i*h;
err=fabs(y-W(t));
if(i%100==0)
printf("%.2lf %10.7lf %10.7lf %10.7lf\n"
,t,y,W(t),err);
}
return;
}
輸出畫面
t y(t) w(t) error
=====================================
0.00 1.0000000 1.0000000 0.0000000
0.10 0.2231302 0.2231302 0.0000000
0.20 0.0497871 0.0497871 0.0000000
0.30 0.0111090 0.0111090 0.0000000
0.40 0.0024788 0.0024788 0.0000000
0.50 0.0005531 0.0005531 0.0000000
0.60 0.0001234 0.0001234 0.0000000
0.70 0.0000275 0.0000275 0.0000000
0.80 0.0000061 0.0000061 0.0000000
0.90 0.0000014 0.0000014 0.0000000
1.00 0.0000003 0.0000003 0.0000000
Command exited with non-zero status 233
https://www.bluffton.edu/homepages/facstaff/nesterd/java/slopefields.html
2019年4月30日 星期二
C語言 例題 5-7 利用 二階 Runge-Kutta 解 二階常微分程式 y'' + 4y' + 4y = 4 cos(t) + 3 sin(t) , y(0)=1 , y'(0)=0
C語言 例題 5-7 利用 二階 Runge-Kutta 解 二階常微分程式
y'' + 4y' + 4y = 4 cos(t) + 3 sin(t) , y(0)=1 , y'(0)=0
設 z= y'
z' + 4z + 4y = 4 cos(t) + 3 sin(t)
z ' = f2( y , z , t) = - 4z - 4y + 4 cos(t) + 3 sin(t)
f' = f1(y,z ,t) = z , y(0)=1
設 y1= y , y2=z
y'1 = y' = f1(y1,y2,t) = y2 , y1(0)=1 << f' = f1(y,z ,t) = z , y(0)=1 >>
y'2 = z' = f2(y1,y2,t) = - 4y2 - 4y1 + 4 cos(t) + 3 sin(t) , y2(0)=0 <<- 4z - 4y + 4 cos(t) + 3 sin(t) >>
/* ex5-7.c based on Second-Order Runge-Kutta Method
* to approximate the solution of the m order
* system of first-order initial-value problem.
* y1=f1(y1,y2,...,ym,t)
* y2=f2(y1,y2,...,ym,t)
* .
* .
* ym=fm(y1,y2,...,ym,t)
* a<=t<=b, y1(a)=y01,y2(a)=y02,...,ym(a)=y0m.
* at (n+1) equally spaced numbers in the interval
* [a,b].
*/
#include <stdio.h>
#include <math.h>
#define f1(y1,y2,t) (y2)
#define f2(y1,y2,t) ((-4.0*y2-4.0*y1)+4*cos(t)+3*sin(t))
void main()
{
int i=0,j,n=4,m=2;
double t,a=0.0,b=0.4,h,k1[10],k2[10],y[10],y0[10];
h=(b-a)/n;
t=a;
y0[1]=1.0;
y0[2]=0.0;
for(j=1;j<=m;j++)
y[j]=y0[j];
printf("\ni =%1d \n",i);
printf("t y1 y2 \n");
printf("=============================\n");
printf("%.2lf %10.8lf %10.8lf \n",t,y0[1],y0[2]);
for(i=1;i<=n;i++)
{
printf("\ni =%1d \n",i);
for(j=1;j<=m;j++)
{
if(j==1)
k1[j]=h*f1(0,y[j+1],0);
else if(j==2)
k1[j]=h*f2(y[j-1],y[j],t);
printf("====================\n");
printf("t k1%1d\n",j);
printf("%.2lf %10.8lf \n",t,k1[j]);
}
for(j=1;j<=m;j++)
{
if(j==1)
k2[j]=h*f1(0,(y[j+1]+k1[j+1]),0);
else if(j==2)
k2[j]=h*f2((y[j-1]+k1[j-1]),(y[j]+k1[j]),(t+h));
printf("====================\n");
printf("t k2%1d\n",j);
printf("%.2lf %10.8lf \n",t+h,k2[j]);
}
for(j=1;j<=m;j++)
y[j]=y[j]+0.5*(k1[j]+k2[j]);
t=a+i*h;
if(i%1==0)
{
printf("\nt y1 y2 \n");
printf("=============================\n");
printf("%.2lf %10.8lf %10.8lf\n\n",t,y[1],y[2]);
}
}
return;
}
輸出畫面
i =0
t y1 y2
=============================
0.00 1.00000000 0.00000000
i =1
====================
t k11
0.00 0.00000000
====================
t k12
0.00 0.00000000
====================
t k21
0.10 0.00000000
====================
t k22
0.10 0.02795169
t y1 y2
=============================
0.10 1.00000000 0.01397585
i =2
====================
t k11
0.10 0.00139758
====================
t k12
0.10 0.02236135
====================
t k21
0.20 0.00363372
====================
t k22
0.20 0.03653352
t y1 y2
=============================
0.20 1.00251565 0.04342328
i =3
====================
t k11
0.20 0.00434233
====================
t k12
0.20 0.03325186
====================
t k21
0.30 0.00766751
====================
t k22
0.30 0.03737741
t y1 y2
=============================
0.30 1.00852057 0.07873791
i =4
====================
t k11
0.30 0.00787379
====================
t k12
0.30 0.03588726
====================
t k21
0.40 0.01146252
====================
t k22
0.40 0.03284208
t y1 y2
=============================
0.40 1.01818873 0.11310259
y'' + 4y' + 4y = 4 cos(t) + 3 sin(t) , y(0)=1 , y'(0)=0
設 z= y'
z' + 4z + 4y = 4 cos(t) + 3 sin(t)
z ' = f2( y , z , t) = - 4z - 4y + 4 cos(t) + 3 sin(t)
f' = f1(y,z ,t) = z , y(0)=1
設 y1= y , y2=z
y'1 = y' = f1(y1,y2,t) = y2 , y1(0)=1 << f' = f1(y,z ,t) = z , y(0)=1 >>
/* ex5-7.c based on Second-Order Runge-Kutta Method
* to approximate the solution of the m order
* system of first-order initial-value problem.
* y1=f1(y1,y2,...,ym,t)
* y2=f2(y1,y2,...,ym,t)
* .
* .
* ym=fm(y1,y2,...,ym,t)
* a<=t<=b, y1(a)=y01,y2(a)=y02,...,ym(a)=y0m.
* at (n+1) equally spaced numbers in the interval
* [a,b].
*/
#include <stdio.h>
#include <math.h>
#define f1(y1,y2,t) (y2)
#define f2(y1,y2,t) ((-4.0*y2-4.0*y1)+4*cos(t)+3*sin(t))
void main()
{
int i=0,j,n=4,m=2;
double t,a=0.0,b=0.4,h,k1[10],k2[10],y[10],y0[10];
h=(b-a)/n;
t=a;
y0[1]=1.0;
y0[2]=0.0;
for(j=1;j<=m;j++)
y[j]=y0[j];
printf("\ni =%1d \n",i);
printf("t y1 y2 \n");
printf("=============================\n");
printf("%.2lf %10.8lf %10.8lf \n",t,y0[1],y0[2]);
for(i=1;i<=n;i++)
{
printf("\ni =%1d \n",i);
for(j=1;j<=m;j++)
{
if(j==1)
k1[j]=h*f1(0,y[j+1],0);
else if(j==2)
k1[j]=h*f2(y[j-1],y[j],t);
printf("====================\n");
printf("t k1%1d\n",j);
printf("%.2lf %10.8lf \n",t,k1[j]);
}
for(j=1;j<=m;j++)
{
if(j==1)
k2[j]=h*f1(0,(y[j+1]+k1[j+1]),0);
else if(j==2)
k2[j]=h*f2((y[j-1]+k1[j-1]),(y[j]+k1[j]),(t+h));
printf("====================\n");
printf("t k2%1d\n",j);
printf("%.2lf %10.8lf \n",t+h,k2[j]);
}
for(j=1;j<=m;j++)
y[j]=y[j]+0.5*(k1[j]+k2[j]);
t=a+i*h;
if(i%1==0)
{
printf("\nt y1 y2 \n");
printf("=============================\n");
printf("%.2lf %10.8lf %10.8lf\n\n",t,y[1],y[2]);
}
}
return;
}
輸出畫面
i =0
t y1 y2
=============================
0.00 1.00000000 0.00000000
i =1
====================
t k11
0.00 0.00000000
====================
t k12
0.00 0.00000000
====================
t k21
0.10 0.00000000
====================
t k22
0.10 0.02795169
t y1 y2
=============================
0.10 1.00000000 0.01397585
i =2
====================
t k11
0.10 0.00139758
====================
t k12
0.10 0.02236135
====================
t k21
0.20 0.00363372
====================
t k22
0.20 0.03653352
t y1 y2
=============================
0.20 1.00251565 0.04342328
i =3
====================
t k11
0.20 0.00434233
====================
t k12
0.20 0.03325186
====================
t k21
0.30 0.00766751
====================
t k22
0.30 0.03737741
t y1 y2
=============================
0.30 1.00852057 0.07873791
i =4
====================
t k11
0.30 0.00787379
====================
t k12
0.30 0.03588726
====================
t k21
0.40 0.01146252
====================
t k22
0.40 0.03284208
t y1 y2
=============================
0.40 1.01818873 0.11310259
數值分析 Numerical Mathematics and Computing Fifth Edition
Numerical Mathematics and Computing
Fifth Edition
源自https://web.ma.utexas.edu/CNA/NMC5/nmc5-C.html
Numerical Mathematics and Computing
Fifth EditionWard Cheney & David Kincaid
Sample C Codes
In the following table, each line/entry contains the program file name, the page number where it can be found in the textbook, and a brief description. Click on the program name to display the source code, which can be downloaded.
| Chapter 1: Introduction | ||
| first.c | 6-7 | First programming experiment |
| double_first.c | 6-7 | First programming experiment (doulbe precision version) |
| pi.c | 8 | Simple code to illustrate double precision |
| Chapter 2: Number Representation and Errors | ||
| xsinx.c | 77-79 | Example of programming f(x) = x - sinx carefully |
| Chapter 3: Locating Roots of Equations | ||
| bisection.c | 94-95 | Bisection method |
| rec_bisection.c | 95-96 | Recursive version of bisection method |
| newton.c | 106-107 | Sample Newton method |
| secant.c | 127 | Secant method |
| Chapter 4: Interpolation and Numerical Differentiation | ||
| coef.c | 152-155 | Newton interpolation polynomial at equidistant pts |
| deriv.c | 185-186 | Derivative by center differences/Richardson extrapolation |
| Chapter 5: Numerical Integration | ||
| sums.c | 200 | Upper/lower sums experiment for an integral |
| trapezoid.c | 207 | Trapezoid rule experiment for an integral |
| romberg.c | 223-224 | Romberg arrays for three separate functions |
| Chapter 6: More on Numerical Integration | ||
| rec_simpson.c | 241 | Adaptive scheme for Simpson's rule |
| Chapter 7: Systems of Linear Equations | ||
| ngauss.c | 270-271 | Naive Gaussian elimination to solve linear systems |
| gauss.c | 285-287 | Gaussian elimination with scaled partial pivoting |
| tri.c | 301-302 | Solves tridiagonal systems |
| penta.c | 204 | Solves pentadiagonal linear systems |
| Chapter 8: More on Systems of Linear Equations | ||
| Chapter 9: Approximation by Spline Functions | ||
| spline1.c | 385 | Interpolates table using a first-degree spline function |
| spline3.c | 404-406 | Natural cubic spline function at equidistant points |
| spline2.c | 427-428 | Interpolates table using a quadratic B-spline function |
| schoenberg.c | 430-431 | Interpolates table using Schoenberg's process |
| Chapter 10: Ordinary Differential Equations | ||
| euler.c | 448-449 | Euler's method for solving an ODE |
| taylor.c | 451 | Taylor series method (order 4) for solving an ODE |
| rk4.c | 462-463 | Runge-Kutta method (order 4) for solving an IVP |
| rk45.c | 472-473 | Runge-Kutta-Fehlberg method for solving an IVP |
| mainrk45.c | 474 | Runge-Kutta-Fehlberg method for solving an IVP (main program) |
| rk45ad.c | 474 | Adaptive Runge-Kutta-Fehlberg method |
| Chapter 11: Systems of Ordinary Differential Equations | ||
| taylorsys.c | 489-491 | Taylor series method (order 4) for systems of ODEs |
| rk4sys.c | 491-493, 496 | Runge-Kutta method (order 4) for systems of ODEs |
| amrk.c | 510-513 | Adams-Moulton method for systems of ODEs |
| amrkad.c | 513 | Adaptive Adams-Moulton method for systems of ODEs |
| Chapter 12: Smoothing of Data and the Method of Least Squares | ||
| Chapter 13: Monte Carlo Methods and Simulation | ||
| test_random.c | 5652-563 | Example to compute, store, and print random numbers |
| coarse_check.c | 564 | Coarse check on the random-number generator |
| double_integral.c | 574-575 | Volume of a complicated 3D region by Monte Carlo |
| volume_region.c | 575-576 | Numerical value of integral over a 2D disk by Monte Carlo |
| cone.c | 576-576 | Ice cream cone example |
| loaded_die.c | 581 | Loaded die problem simulation |
| birthday.c | 583 | Birthday problem simulation |
| needle.c | 584 | Buffon's needle problem simulation |
| two_die.c | 585 | Two dice problem simulation |
| shielding.c | 586-587 | Neutron shielding problem simulation |
| Chapter 14: Boundary Value Problems for Ordinary Differential Equations | ||
| bvp1.c | 602-603 | Boundary value problem solved by discretization technique |
| bvp2.c | 605-606 | Boundary value problem solved by shooting method |
| Chapter 15: Partial Differential Equations | ||
| parabolic1.c | 618-619 | Parabolic partial differential equation problem |
| parabolic2.c | 620-621 | Parabolic PDE problem solved by Crank-Nicolson method |
| hyperbolic.c | 633-634 | Hyperbolic PDE problem solved by discretization |
| seidel.c | 642-645 | Elliptic PDE solved by discretization/ Gauss-Seidel method |
| Chapter 16: Minimization of Functions | ||
| Chapter 17: Linear Programming | ||
ftp://ftp.ma.utexas.edu/pub/cheney-kincaid/
| [Home] | [Features] | [TOC] | [Purchase] | [ Sample Code] | [ Web] | [ Manuals] | [Errata] | [Links] |
| Last updated: |
C語言 例題5-6 四階 Runge-Kutta 解 ODE y'= -y + t^2 + 1 , 0<=t<=1 , y(0)=1 , 真實解 W(t)= -2e^(-t) + t ^2 - 2t + 3
C語言 例題5-6 四階 Runge-Kutta 解 ODE y'= -y + t^2 + 1 , 0<=t<=1 , y(0)=1 , 真實解 W(t)= -2e^(-t) + t ^2 - 2t + 3
/* ex5-6.c based on Four-Order Runge-Kutta
* Method to approximate the solution of the
* initial-value problem
* y'=f(y,t), a<=t<=b, y(a)=y0
* at (n+1) equally spaced numbers in the interval
* [a,b]: input a,b,n,and initial condition y0.
*/
#include <stdio.h>
#include <math.h>
#define F(y,t) (-y+t*t+1)
#define W(t) (-2*(1/exp(t))+pow(t,2)-2*t+3)
void main()
{
int i,n=100;
double a=0.0,b=1.0,y0=1.0,k1,k2,k3,k4,h,t,y,err;
h=(b-a)/n;
t=a;
y=y0;
err=fabs(y-W(t));
printf("t y(t) w(t) error\n");
printf("=====================================\n");
printf("%.2lf %10.7lf %10.7lf %10.7lf\n",t,y,W(t),err);
for(i=1;i<=n;i++)
{
k1=h*F(y,t);
k2=h*F((y+k1/2.0),(t+h/2.0));
k3=h*F((y+k2/2.0),(t+h/2.0));
k4=h*F((y+k3),(t+h));
y=y+(k1+2*k2+2*k3+k4)/6.0;
t=a+i*h;
err=fabs(y-W(t));
if(i%10==0)
printf("%.2lf %10.7lf %10.7lf %10.7lf\n",t,y,W(t),err);
}
return;
}
輸出畫面
t y(t) w(t) error
=====================================
0.00 1.0000000 1.0000000 0.0000000
0.10 1.0003252 1.0003252 0.0000000
0.20 1.0025385 1.0025385 0.0000000
0.30 1.0083636 1.0083636 0.0000000
0.40 1.0193599 1.0193599 0.0000000
0.50 1.0369387 1.0369387 0.0000000
0.60 1.0623767 1.0623767 0.0000000
0.70 1.0968294 1.0968294 0.0000000
0.80 1.1413421 1.1413421 0.0000000
0.90 1.1968607 1.1968607 0.0000000
1.00 1.2642411 1.2642411 0.0000000
Command exited with non-zero status 101
/* ex5-6.c based on Four-Order Runge-Kutta
* Method to approximate the solution of the
* initial-value problem
* y'=f(y,t), a<=t<=b, y(a)=y0
* at (n+1) equally spaced numbers in the interval
* [a,b]: input a,b,n,and initial condition y0.
*/
#include <stdio.h>
#include <math.h>
#define F(y,t) (-y+t*t+1)
#define W(t) (-2*(1/exp(t))+pow(t,2)-2*t+3)
void main()
{
int i,n=100;
double a=0.0,b=1.0,y0=1.0,k1,k2,k3,k4,h,t,y,err;
h=(b-a)/n;
t=a;
y=y0;
err=fabs(y-W(t));
printf("t y(t) w(t) error\n");
printf("=====================================\n");
printf("%.2lf %10.7lf %10.7lf %10.7lf\n",t,y,W(t),err);
for(i=1;i<=n;i++)
{
k1=h*F(y,t);
k2=h*F((y+k1/2.0),(t+h/2.0));
k3=h*F((y+k2/2.0),(t+h/2.0));
k4=h*F((y+k3),(t+h));
y=y+(k1+2*k2+2*k3+k4)/6.0;
t=a+i*h;
err=fabs(y-W(t));
if(i%10==0)
printf("%.2lf %10.7lf %10.7lf %10.7lf\n",t,y,W(t),err);
}
return;
}
輸出畫面
t y(t) w(t) error
=====================================
0.00 1.0000000 1.0000000 0.0000000
0.10 1.0003252 1.0003252 0.0000000
0.20 1.0025385 1.0025385 0.0000000
0.30 1.0083636 1.0083636 0.0000000
0.40 1.0193599 1.0193599 0.0000000
0.50 1.0369387 1.0369387 0.0000000
0.60 1.0623767 1.0623767 0.0000000
0.70 1.0968294 1.0968294 0.0000000
0.80 1.1413421 1.1413421 0.0000000
0.90 1.1968607 1.1968607 0.0000000
1.00 1.2642411 1.2642411 0.0000000
Command exited with non-zero status 101
C語言 例題5-5.c 使用 二階Runge-Kutta 解 ODE y'= -y + t^2 + 1 , 0<=t<=1 , y(0)=1 , 真實解 W(t)= -2e^(-t) + t ^2 - 2t + 3
C語言 例題5-5 使用 二階Runge-Kutta 解 ODE y'= -y + t^2 + 1 , 0<=t<=1 , y(0)=1 , 真實解 W(t)= -2e^(-t) + t ^2 - 2t + 3
/* ex5-5.c Second Order Runge-Kutta Method is used
* for solving Ordinary Differential Equation of
* y'=f(y,t) with initial condition of y(t0)=y0.
*/
#include <stdio.h>
#include <math.h>
#define F(y,t) (-y+t*t+1)
#define W(t) (-2*(1.0/exp(t))+pow(t,2)-2*t+3)
void main()
{
int i,n=100;
double h,a=0.0,b=1.0,t0,t,y0=1.0,y,k1,k2;
h=(b-a)/n;
y=y0;
t0=a;
t=t0;
printf("t y(t) w(t) error\n");
printf("=====================================\n");
printf("%.2lf %10.7lf %10.7lf %10.7lf\n", t,y,W(t),fabs(y-W(t)));
for(i=1;i<=n;i++)
{
k1=h*F(y,t);
k2=h*F((y+k1),(t+h));
y=y+0.5*(k1+k2);
t=t+h;
if(i%10==0)
printf("%.2lf %10.7lf %10.7lf %10.7lf\n", t,y,W(t),fabs(y-W(t)));
}
return;
}
輸出畫面
t y(t) w(t) error
=====================================
0.00 1.0000000 1.0000000 0.0000000
0.10 1.0003269 1.0003252 0.0000017
0.20 1.0025421 1.0025385 0.0000036
0.30 1.0083691 1.0083636 0.0000056
0.40 1.0193675 1.0193599 0.0000076
0.50 1.0369483 1.0369387 0.0000096
0.60 1.0623883 1.0623767 0.0000116
0.70 1.0968430 1.0968294 0.0000136
0.80 1.1413577 1.1413421 0.0000156
0.90 1.1968782 1.1968607 0.0000175
1.00 1.2642605 1.2642411 0.0000194
Command exited with non-zero status 101
/* ex5-5.c Second Order Runge-Kutta Method is used
* for solving Ordinary Differential Equation of
* y'=f(y,t) with initial condition of y(t0)=y0.
*/
#include <stdio.h>
#include <math.h>
#define F(y,t) (-y+t*t+1)
#define W(t) (-2*(1.0/exp(t))+pow(t,2)-2*t+3)
void main()
{
int i,n=100;
double h,a=0.0,b=1.0,t0,t,y0=1.0,y,k1,k2;
h=(b-a)/n;
y=y0;
t0=a;
t=t0;
printf("t y(t) w(t) error\n");
printf("=====================================\n");
printf("%.2lf %10.7lf %10.7lf %10.7lf\n", t,y,W(t),fabs(y-W(t)));
for(i=1;i<=n;i++)
{
k1=h*F(y,t);
k2=h*F((y+k1),(t+h));
y=y+0.5*(k1+k2);
t=t+h;
if(i%10==0)
printf("%.2lf %10.7lf %10.7lf %10.7lf\n", t,y,W(t),fabs(y-W(t)));
}
return;
}
輸出畫面
t y(t) w(t) error
=====================================
0.00 1.0000000 1.0000000 0.0000000
0.10 1.0003269 1.0003252 0.0000017
0.20 1.0025421 1.0025385 0.0000036
0.30 1.0083691 1.0083636 0.0000056
0.40 1.0193675 1.0193599 0.0000076
0.50 1.0369483 1.0369387 0.0000096
0.60 1.0623883 1.0623767 0.0000116
0.70 1.0968430 1.0968294 0.0000136
0.80 1.1413577 1.1413421 0.0000156
0.90 1.1968782 1.1968607 0.0000175
1.00 1.2642605 1.2642411 0.0000194
Command exited with non-zero status 101
2019年4月28日 星期日
C語言 例題5-4 二階 Runge-Kutta 解ODE y'= -y + t +1 , 0<=t <= 1 , y(1)=?
C語言 例題5-4 二階 Runge-Kutta 解ODE y'= -y + t +1 , 0<=t <= 1 , y(1)=?
#include<stdio.h>
#include <math.h>
/*
Enter the value of x0: 0
Enter the value of y0: 2
Enter the value of h: 0.05
Enter the value of last point: 0.1
*/
//dy/dx = y - x
#define F(x,y) (-y+x+1)
void main()
{
double y0,x0,y1,n,h,f,f1,k1,k2;
int i=0;
x0=0.0;
y0=1.0;
h=0.2;
n=1.0;
printf("\nEnter the value of x0:%1.2lf",x0 );
printf("\nEnter the value of y0:%1.2lf",y0 );
printf("\nEnter the value of h:%1.2lf",h );
printf("\nEnter the value of last point:%1.2lf",n);
for(; x0<n; x0=x0+h)
{
f=F(x0,y0);
k1 = h * f;
f1 = F(x0+h,y0+k1);
k2 = h * f1;
y1 = y0 + ( k1 + k2)/2;
printf("\n i = %2d ",i);
printf("\n k1 = %.4lf ",k1);
printf("\n k2 = %.4lf ",k2);
printf("\n y(%.4lf) = %.3lf ",x0+h,y1);
y0=y1;
i++;
}
}
輸出畫面
Enter the value of x0:0.00
Enter the value of y0:1.00
Enter the value of h:0.20
Enter the value of last point:1.00
i = 0
k1 = 0.0000
k2 = 0.0400
y(0.2000) = 1.020
i = 1
k1 = 0.0360
k2 = 0.0832
y(0.4000) = 1.080
i = 2
k1 = 0.0641
k2 = 0.1169
y(0.6000) = 1.170
i = 3
k1 = 0.0860
k2 = 0.1432
y(0.8000) = 1.285
i = 4
k1 = 0.1031
k2 = 0.1637
y(1.0000) = 1.418
#include<stdio.h>
#include <math.h>
/*
Enter the value of x0: 0
Enter the value of y0: 2
Enter the value of h: 0.05
Enter the value of last point: 0.1
*/
//dy/dx = y - x
#define F(x,y) (-y+x+1)
void main()
{
double y0,x0,y1,n,h,f,f1,k1,k2;
int i=0;
x0=0.0;
y0=1.0;
h=0.2;
n=1.0;
printf("\nEnter the value of x0:%1.2lf",x0 );
printf("\nEnter the value of y0:%1.2lf",y0 );
printf("\nEnter the value of h:%1.2lf",h );
printf("\nEnter the value of last point:%1.2lf",n);
for(; x0<n; x0=x0+h)
{
f=F(x0,y0);
k1 = h * f;
f1 = F(x0+h,y0+k1);
k2 = h * f1;
y1 = y0 + ( k1 + k2)/2;
printf("\n i = %2d ",i);
printf("\n k1 = %.4lf ",k1);
printf("\n k2 = %.4lf ",k2);
printf("\n y(%.4lf) = %.3lf ",x0+h,y1);
y0=y1;
i++;
}
}
輸出畫面
Enter the value of x0:0.00
Enter the value of y0:1.00
Enter the value of h:0.20
Enter the value of last point:1.00
i = 0
k1 = 0.0000
k2 = 0.0400
y(0.2000) = 1.020
i = 1
k1 = 0.0360
k2 = 0.0832
y(0.4000) = 1.080
i = 2
k1 = 0.0641
k2 = 0.1169
y(0.6000) = 1.170
i = 3
k1 = 0.0860
k2 = 0.1432
y(0.8000) = 1.285
i = 4
k1 = 0.1031
k2 = 0.1637
y(1.0000) = 1.418
C語言 4階 Runge-Kutta Method 求ODE y'= (x-y)/(x+y) y(2) = ??
C語言 例題 5-4 4階 Runge-Kutta Method 求ODE y'= (x-y)/(x+y) y(2) = ??
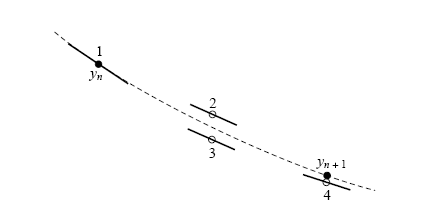
4th Order Runge-Kutta Method
源自
http://boson4.phys.tku.edu.tw/numerical_methods/nm_units/ODE_Runge-Kutta.htm
最常用且通用的 RK 方法是四階的,我們可以想見它是由更多不同樣式的半步組合所構成,其中並包含了原有的起點處定斜率與終點處定斜率,請注意這裏 k1、k2、k3、k4 的定義與其相依性(即 k4 用到 k3、k3 用到 k2、k2 用到 k1 的狀況)
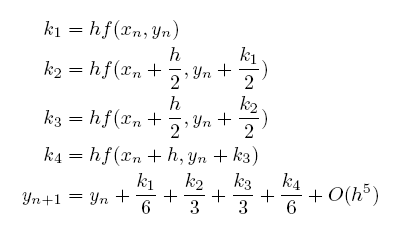 (事實上)這裏的圖是有印錯的情況,我認為 2 與 3 的標注處應該對調,公式中的 k1、k2、k3、k4 全部都有 h ,但分別是乘以 (a) 在起點處 1 求的斜率、(b) 以起點斜率走半步到 2 處求斜率、(c) 一樣從起點開始但,改採前面的半步處 2 之斜率,重走半步到 3 後求斜率,以及最後 (d) 採用上一個於 3 處所獲得的斜率,從起點出發走一整步到 4 處求斜率。
(事實上)這裏的圖是有印錯的情況,我認為 2 與 3 的標注處應該對調,公式中的 k1、k2、k3、k4 全部都有 h ,但分別是乘以 (a) 在起點處 1 求的斜率、(b) 以起點斜率走半步到 2 處求斜率、(c) 一樣從起點開始但,改採前面的半步處 2 之斜率,重走半步到 3 後求斜率,以及最後 (d) 採用上一個於 3 處所獲得的斜率,從起點出發走一整步到 4 處求斜率。
#include<stdio.h>
#include<math.h>
float f(float x,float y);
int main()
{
float x0,y0,m1,m2,m3,m4,m,y,x,h,xn;
x0=0.0;
y0=2.0;
xn=2.0;
h=0.5;
printf("x0=%1.1lf ,y0=%1.1lf ,xn=%1.1lf ,h=%1.1lf",x0,y0,xn,h);
x=x0;
y=y0;
printf("\n\nX\t\t Y\n");
printf("======================\n");
while(x<xn)
{
m1=f(x0,y0);
m2=f((x0+h/2.0),(y0+m1*h/2.0));
m3=f((x0+h/2.0),(y0+m2*h/2.0));
m4=f((x0+h),(y0+m3*h));
m=((m1+2*m2+2*m3+m4)/6);
y=y+m*h;
x=x+h;
printf("%f\t%f\n",x,y);
}
}
float f(float x,float y)
{
float m;
m=(x-y)/(x+y);
return m;
}
輸出畫面
x0=0.0 ,y0=2.0 ,xn=2.0 ,h=0.5
X Y
======================
0.500000 1.621356
1.000000 1.242713
1.500000 0.864069
2.000000 0.485426
4th Order Runge-Kutta Method
源自
http://boson4.phys.tku.edu.tw/numerical_methods/nm_units/ODE_Runge-Kutta.htm
最常用且通用的 RK 方法是四階的,我們可以想見它是由更多不同樣式的半步組合所構成,其中並包含了原有的起點處定斜率與終點處定斜率,請注意這裏 k1、k2、k3、k4 的定義與其相依性(即 k4 用到 k3、k3 用到 k2、k2 用到 k1 的狀況)
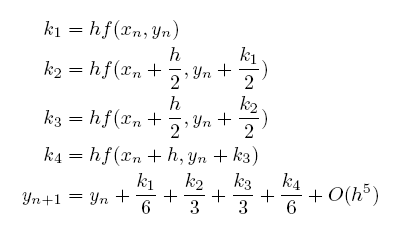

#include<stdio.h>
#include<math.h>
float f(float x,float y);
int main()
{
float x0,y0,m1,m2,m3,m4,m,y,x,h,xn;
x0=0.0;
y0=2.0;
xn=2.0;
h=0.5;
printf("x0=%1.1lf ,y0=%1.1lf ,xn=%1.1lf ,h=%1.1lf",x0,y0,xn,h);
x=x0;
y=y0;
printf("\n\nX\t\t Y\n");
printf("======================\n");
while(x<xn)
{
m1=f(x0,y0);
m2=f((x0+h/2.0),(y0+m1*h/2.0));
m3=f((x0+h/2.0),(y0+m2*h/2.0));
m4=f((x0+h),(y0+m3*h));
m=((m1+2*m2+2*m3+m4)/6);
y=y+m*h;
x=x+h;
printf("%f\t%f\n",x,y);
}
}
float f(float x,float y)
{
float m;
m=(x-y)/(x+y);
return m;
}
輸出畫面
x0=0.0 ,y0=2.0 ,xn=2.0 ,h=0.5
X Y
======================
0.500000 1.621356
1.000000 1.242713
1.500000 0.864069
2.000000 0.485426
C語言 例題5-3 使用 Euler修正法 ,求ODE y'=y+2 e^(4t) y(0)=-3 , 0<= t <=1 y(1)=??
C語言 例題5-3 使用 Euler修正法 ,求ODE
y'=y+2 e^(4t) y(0)=-3 , 0<= t <=1
// C code for solving the differential equation
// using Predictor-Corrector or Modified-Euler method
// with the given conditions, y(0) = 0.5, step size(h) = 0.2
// to find y(1)
#include <stdio.h>
#include <math.h>
// consider the differential equation
// for a given x and y, return v
double f(double x, double y)
{
double v = y + 2 * exp(4*x) ;
return v;
}
// predicts the next value for a given (x, y)
// and step size h using Euler method
double predict(double x, double y, double h)
{
// value of next y(predicted) is returned
double y1p = y + h * f(x, y);
return y1p;
}
// corrects the predicted value
// using Modified Euler method
double correct(double x, double y, double x1, double y1,double h)
{
// (x, y) are of previous step
// and x1 is the increased x for next step
// and y1 is predicted y for next step
double e = 0.00001;
double y1c = y1;
do {
y1 = y1c;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
} while (fabs(y1c - y1) > e);
// every iteration is correcting the value
// of y using average slope
return y1c;
}
void printFinalValues(double x, double xn, double y, double h)
{
int i=1;
while (x < xn) {
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
if (i%10==0)
{
printf(" predict----The value of y , at x = %2.4lf is :%2.4lf\n " ,x1 ,y1p);
printf(" correct----The value of y , at x = %2.4lf is :%2.4lf\n " ,x1 ,y1c);
}
x = x1;
y = y1c;
i++;
}
// at every iteration first the value
// of for next step is first predicted
// and then corrected.
printf("\n\nThe final value of y , at x = %2.4lf is :%2.4lf " ,x ,y);
}
int main()
{
// here x and y are the initial
// given condition, so x=0 and y=0.5
double x = 0, y = -3;
// final value of x for which y is needed
double xn = 1;
// step size
double h = 0.01;
printFinalValues(x, xn, y, h);
return 0;
}
輸出畫面
predict----The value of y , at x = 0.1000 is :-3.0583 ---修正前
correct----The value of y , at x = 0.1000 is :-3.0577 ---修正後
predict----The value of y , at x = 0.2000 is :-2.9956
correct----The value of y , at x = 0.2000 is :-2.9947
predict----The value of y , at x = 0.3000 is :-2.7373
correct----The value of y , at x = 0.3000 is :-2.7359
predict----The value of y , at x = 0.4000 is :-2.1699
correct----The value of y , at x = 0.4000 is :-2.1676
predict----The value of y , at x = 0.5000 is :-1.1222
correct----The value of y , at x = 0.5000 is :-1.1186
predict----The value of y , at x = 0.6000 is :0.6633
correct----The value of y , at x = 0.6000 is :0.6687
predict----The value of y , at x = 0.7000 is :3.5728
correct----The value of y , at x = 0.7000 is :3.5810
predict----The value of y , at x = 0.8000 is :8.1849
correct----The value of y , at x = 0.8000 is :8.1973
predict----The value of y , at x = 0.9000 is :15.3656
correct----The value of y , at x = 0.9000 is :15.3843
predict----The value of y , at x = 1.0000 is :26.4097
correct----The value of y , at x = 1.0000 is :26.4378
The final value of y , at x = 1.0000 is :26.4378
The final value of y , at x = 1.0000 is :26.4378
y'=y+2 e^(4t) y(0)=-3 , 0<= t <=1
// C code for solving the differential equation
// using Predictor-Corrector or Modified-Euler method
// with the given conditions, y(0) = 0.5, step size(h) = 0.2
// to find y(1)
#include <stdio.h>
#include <math.h>
// consider the differential equation
// for a given x and y, return v
double f(double x, double y)
{
double v = y + 2 * exp(4*x) ;
return v;
}
// predicts the next value for a given (x, y)
// and step size h using Euler method
double predict(double x, double y, double h)
{
// value of next y(predicted) is returned
double y1p = y + h * f(x, y);
return y1p;
}
// corrects the predicted value
// using Modified Euler method
double correct(double x, double y, double x1, double y1,double h)
{
// (x, y) are of previous step
// and x1 is the increased x for next step
// and y1 is predicted y for next step
double e = 0.00001;
double y1c = y1;
do {
y1 = y1c;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
} while (fabs(y1c - y1) > e);
// every iteration is correcting the value
// of y using average slope
return y1c;
}
void printFinalValues(double x, double xn, double y, double h)
{
int i=1;
while (x < xn) {
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
if (i%10==0)
{
printf(" predict----The value of y , at x = %2.4lf is :%2.4lf\n " ,x1 ,y1p);
printf(" correct----The value of y , at x = %2.4lf is :%2.4lf\n " ,x1 ,y1c);
}
x = x1;
y = y1c;
i++;
}
// at every iteration first the value
// of for next step is first predicted
// and then corrected.
printf("\n\nThe final value of y , at x = %2.4lf is :%2.4lf " ,x ,y);
}
int main()
{
// here x and y are the initial
// given condition, so x=0 and y=0.5
double x = 0, y = -3;
// final value of x for which y is needed
double xn = 1;
// step size
double h = 0.01;
printFinalValues(x, xn, y, h);
return 0;
}
輸出畫面
predict----The value of y , at x = 0.1000 is :-3.0583 ---修正前
correct----The value of y , at x = 0.1000 is :-3.0577 ---修正後
predict----The value of y , at x = 0.2000 is :-2.9956
correct----The value of y , at x = 0.2000 is :-2.9947
predict----The value of y , at x = 0.3000 is :-2.7373
correct----The value of y , at x = 0.3000 is :-2.7359
predict----The value of y , at x = 0.4000 is :-2.1699
correct----The value of y , at x = 0.4000 is :-2.1676
predict----The value of y , at x = 0.5000 is :-1.1222
correct----The value of y , at x = 0.5000 is :-1.1186
predict----The value of y , at x = 0.6000 is :0.6633
correct----The value of y , at x = 0.6000 is :0.6687
predict----The value of y , at x = 0.7000 is :3.5728
correct----The value of y , at x = 0.7000 is :3.5810
predict----The value of y , at x = 0.8000 is :8.1849
correct----The value of y , at x = 0.8000 is :8.1973
predict----The value of y , at x = 0.9000 is :15.3656
correct----The value of y , at x = 0.9000 is :15.3843
predict----The value of y , at x = 1.0000 is :26.4097
correct----The value of y , at x = 1.0000 is :26.4378
The final value of y , at x = 1.0000 is :26.4378
The final value of y , at x = 1.0000 is :26.4378
C語言 例題5-3 利用Euler修正法求ODE y' = y -2x^2 +1 , y(1) = ?
Euler修正法
For a given differential equation  with initial condition
with initial condition 
find the approximate solution using Predictor-Corrector method.
find the approximate solution using Predictor-Corrector method.
Predictor-Corrector Method :
The predictor-corrector method is also known as Modified-Euler method.
In the Euler method, the tangent is drawn at a point and slope is calculated for a given step size. Thus this method works best with linear functions, but for other cases, there remains a truncation error. To solve this problem the Modified Euler method is introduced. In this method instead of a point, the arithmetic average of the slope over an interval is used.
is used.
The predictor-corrector method is also known as Modified-Euler method.
In the Euler method, the tangent is drawn at a point and slope is calculated for a given step size. Thus this method works best with linear functions, but for other cases, there remains a truncation error. To solve this problem the Modified Euler method is introduced. In this method instead of a point, the arithmetic average of the slope over an interval
Thus in the Predictor-Corrector method for each step the predicted value of  is calculated first using Euler’s method and then the slopes at the points
is calculated first using Euler’s method and then the slopes at the points  and
and  is calculated and the arithmetic average of these slopes are added to
is calculated and the arithmetic average of these slopes are added to  to calculate the corrected value of
to calculate the corrected value of  .
.
So,
here h is step size for each increment
As, in this method, the average slope is used, so the error is reduced significantly. Also, we can repeat the process of correction for convergence. Thus at every step, we are reducing the error thus by improving the value of y.
Input : eq =  , y(0) = 0.5, step size(h) = 0.2
, y(0) = 0.5, step size(h) = 0.2
To find: y(1)
Output: y(1) = 2.18147
To find: y(1)
Output: y(1) = 2.18147
// C++ code for solving the differential equation
// using Predictor-Corrector or Modified-Euler method
// with the given conditions, y(0) = 0.5, step size(h) = 0.2
// to find y(1)
#include <bits/stdc++.h>
using namespace std;
// consider the differential equation
// for a given x and y, return v
double f(double x, double y)
{
double v = y - 2 * x * x + 1;
return v;
}
// predicts the next value for a given (x, y)
// and step size h using Euler method
double predict(double x, double y, double h)
{
// value of next y(predicted) is returned
double y1p = y + h * f(x, y);
return y1p;
}
// corrects the predicted value
// using Modified Euler method
double correct(double x, double y,
double x1, double y1,
double h)
{
// (x, y) are of previous step
// and x1 is the increased x for next step
// and y1 is predicted y for next step
double e = 0.00001;
double y1c = y1;
do {
y1 = y1c;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
} while (fabs(y1c - y1) > e);
// every iteration is correcting the value
// of y using average slope
return y1c;
}
void printFinalValues(double x, double xn,
double y, double h)
{
while (x < xn) {
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
x = x1;
y = y1c;
}
// at every iteration first the value
// of for next step is first predicted
// and then corrected.
cout << "The final value of y at x = "
<< x << " is : " << y << endl;
}
int main()
{
// here x and y are the initial
// given condition, so x=0 and y=0.5
double x = 0, y = 0.5;
// final value of x for which y is needed
double xn = 1;
// step size
double h = 0.2;
printFinalValues(x, xn, y, h);
return 0;
}
輸出畫面
The final value of y at x = 1 is : 2.18147 ...Program finished with exit code 0
Press ENTER to exit console.
C語言
// C code for solving the differential equation
// using Predictor-Corrector or Modified-Euler method
// with the given conditions, y(0) = 0.5, step size(h) = 0.2
// to find y(1)
#include <stdio.h>
#include <math.h>
// consider the differential equation
// for a given x and y, return v
double f(double x, double y)
{
double v = y - 2 * x * x + 1;
return v;
}
// predicts the next value for a given (x, y)
// and step size h using Euler method
double predict(double x, double y, double h)
{
// value of next y(predicted) is returned
double y1p = y + h * f(x, y);
return y1p;
}
// corrects the predicted value
// using Modified Euler method
double correct(double x, double y, double x1, double y1,double h)
{
// (x, y) are of previous step
// and x1 is the increased x for next step
// and y1 is predicted y for next step
double e = 0.00001;
double y1c = y1;
do {
y1 = y1c;
y1c = y + 0.5 * h * (f(x, y) + f(x1, y1));
} while (fabs(y1c - y1) > e);
// every iteration is correcting the value
// of y using average slope
return y1c;
}
void printFinalValues(double x, double xn, double y, double h)
{
while (x < xn) {
double x1 = x + h;
double y1p = predict(x, y, h);
double y1c = correct(x, y, x1, y1p, h);
x = x1;
y = y1c;
}
// at every iteration first the value
// of for next step is first predicted
// and then corrected.
printf("The final value of y , at x = %2.4lf is :%2.4lf " ,x ,y);
}
int main()
{
// here x and y are the initial
// given condition, so x=0 and y=0.5
double x = 0, y = 0.5;
// final value of x for which y is needed
double xn = 1;
// step size
double h = 0.2;
printFinalValues(x, xn, y, h);
return 0;
}
訂閱:
意見 (Atom)
ESP32 (ESP-IDF in VS Code) MFRC522 + MQTT + PYTHON TKinter +SQLite
ESP32 (ESP-IDF in VS Code) MFRC522 + MQTT + PYTHON TKinter +SQLite ESP32 VS Code 程式 ; PlatformIO Project Configuration File ; ; Build op...

-
python pip 不是内部或外部命令 -- 解決方法 要安裝 Pyqt5 1. 首先,開啟命令提示字元。 2. 輸入 pip3 install pyqt5 好像不能執行 ! ! 錯誤顯示 : ‘ pip3 ’ 不是內部或外部命令、可執行的程式或批...
-
課程講義 下載 11/20 1) PPT 下載 + 程式下載 http://www.mediafire.com/file/cru4py7e8pptfda/106%E5%8B%A4%E7%9B%8A2-1.rar 11/27 2) PPT 下載...
-
• 認 識 PreFix、InFix、PostFix PreFix(前序式):* + 1 2 + 3 4 InFix(中序式): (1+2)*(3+4) PostFix(後序式):1 2 + 3 4 + * 後 序式的運算 例如: 運算時由 後序式的...

