已知2點座標
x f(x)
================
0 0
1 -3
求 x=0.5 f(x)= ??
Interpolation is an estimation of a value within two known values in a sequence of values.
Newton’s divided difference interpolation formula is a interpolation technique used when the interval difference is not same for all sequence of values.
Suppose f(x0), f(x1), f(x2)………f(xn) be the (n+1) values of the function y=f(x) corresponding to the arguments x=x0, x1, x2…xn, where interval differences are not same
Then the first divided difference is given by
Then the first divided difference is given by
The second divided difference is given by
and so on…
Divided differences are symmetric with respect to the arguments i.e independent of the order of arguments.
so,
f[x0, x1]=f[x1, x0]
f[x0, x1, x2]=f[x2, x1, x0]=f[x1, x2, x0]
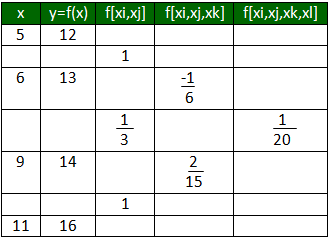
By using first divided difference, second divided difference as so on .A table is formed which is called the divided difference table.
Divided differences are symmetric with respect to the arguments i.e independent of the order of arguments.
so,
f[x0, x1]=f[x1, x0]
f[x0, x1, x2]=f[x2, x1, x0]=f[x1, x2, x0]
By using first divided difference, second divided difference as so on .A table is formed which is called the divided difference table.
Divided difference table:


NEWTON’S DIVIDED DIFFERENCE INTERPOLATION FORMULA
Examples:
Input : Value at 7
 Output :
Output :
 Value at 7 is 13.47
Value at 7 is 13.47
Newton’s Divided Difference formula was put forward to overcome a few limitations of Lagrange’s formula. In Lagrange’s formula, if another interpolation value were to be inserted, then the interpolation coefficients were to be calculated again. This is not the case in Divided Difference. In this tutorial, we’re going to discuss a source code in C for Newton Divided Difference formula along with sample output.
Newton’s Divided Difference Formula eliminates the drawback of recalculation and recomputation of interpolation coefficients by using Newton’s general interpolation formula which uses “divided differences”. Before going through the source code for Newton Divided Difference in C, here’s a brief explanation of what divided differences are with the formula for divided differences.
If (x0,y0), (x1,y1), (x2,y2) …… be given points, then the first divided difference for the arguments x0, x1 is defined as: [x0, x1] = (y1-y0)/(x1-x0). And, similarly, [x1, x2] = (y2-y1)/(x2-x1), and after that [x2, x3] = (y3-y2)/(x3-x2), and so on.
已知2點座標
x f(x)
================
0 0
1 -3
求 x=0.5 f(x)= ??
#/***** Newton Divided Difference interpolation in Python *******/
import math
n=2
x= [0.0 for i in range(n+1)] #x [n] 矩陣
y= [0.0 for i in range(n+1)] #y [n] 矩陣
p =[0.0 for i in range(n+1)] #pf [n] 矩陣
x=[0.0 , 0.0 , 1.0 , 0.0 ]
y=[0.0 , 0.0 , -3.0 , 0.0 ]
k=0.5
print("\nEnter the number of observations:",n )
print("\nEnter the different values of x:\n");
for i in range (1,n+1) : #
print( round( x[i],4),"\t",end='')
print()
print("\nThe corresponding values of y are:\n");
for i in range (1,n+1) : #
print( round(y[i],4),"\t",end='')
print()
print("\nEnter the value of 'k' in f(k) you want to evaluate:" , k)
j=1
f1=1
f2=0;
f=y[1]
while(n !=1):
for i in range (1,n):
p[i] = ((y[i+1]-y[i])/(x[i+j]-x[i]))
y[i]=p[i]
f1=1;
for i in range (1 , j+1):
f1*=(k-x[i])
f2+=(y[1]*f1)
n=n-1
j=j+1
f+=f2
print("\nf {%.2f} = (%.6f) " %(k , f))
輸出畫面
===== RESTART: F:/2018-09勤益科大數值分析/數值分析/PYTHON/EX1-6.py ======
Enter the number of observations: 2
Enter the different values of x:
0.0 1.0
The corresponding values of y are:
0.0 -3.0
Enter the value of 'k' in f(k) you want to evaluate: 0.5
f {0.50} = (-1.500000)
>>>


沒有留言:
張貼留言