Bottom-Up Methodology Design and simulate Full-Adder using 2 Half-Adder and or gate .
Example-2: Design a full adder by using two half adder.
Truth table is given below:
By observing truth table for full adder we can deduce its output boolean expression given below:
Sum ===A′B′C+A′BC′+AB′C′+ABCA′(B′C+BC′)+A(B′C′+BC)=A(B⊕C)+A′(B⊕C¯¯¯¯¯¯¯¯¯¯¯¯¯)A⊕B⊕C Carry ===A′BC+AB′C+ABC′+ABCC(A′B+AB′)+AB(C′+C)C(A⊕B)+AB
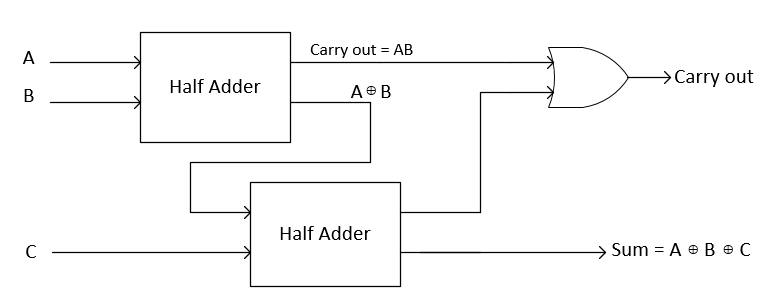
As we can clearly see from boolean expressions that full adder can be constructed by using two half adders. A block diagram for this is shown below:
By using hierarchical style coding we can construct full adder using two half adder as shown in the block diagram above
Verilog Code:
1
2
3
4
5
6
7
8
| module full_adder_join(fsum, fcarry_out, a, b, c);
input a, b, c;
output fsum, fcarry_out;
wire half_sum_1, half_carry_1, half_carry_2;
half_adder HA1(half_sum_1, half_carry_1, a, b); //instance 1 of Half Adder
half_adder HA2(fsum, half_carry_2, half_sum_1, c); //instance 2 of Half Adder
or or1(fcarry_out, half_carry_2, half_carry_1);
endmodule
module half_adder(sum, hcarry, a, b);
input a, b;
output sum, hcarry;
xor sum1(sum, a, b);
and carry1(hcarry, a, b);
endmodule
|
where half adders code are already mentioned in Example-1. Note that we have called half adder 2 times as shown in block diagram as well. This will create two instance of the same module.
Test Bench Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| `timescale 100ns / 10ns
module full_adder_2_HA_tb;
wire t_out_sum, t_out_carry;
reg t_a, t_b, t_c;
full_adder_join UUT(.a(t_a), .b(t_b), .c(t_c), .fsum(t_out_sum), .fcarry_out(t_out_carry));
initial
begin // 1
t_a = 1'b0; t_b = 1'b0; t_c = 1'b0;
#20 //2
t_a = 1'b0; t_b = 1'b0; t_c = 1'b1;
#20 //3
t_a = 1'b0; t_b = 1'b1; t_c = 1'b0;
#20 //4
t_a = 1'b0; t_b = 1'b1; t_c = 1'b1;
#20 //5
t_a = 1'b1; t_b = 1'b0; t_c = 1'b0;
#20 //6
t_a = 1'b1; t_b = 1'b0; t_c = 1'b1;
#20 //7
t_a = 1'b1; t_b = 1'b1; t_c = 1'b0;
#20 //8
t_a = 1'b1; t_b = 1'b1; t_c = 1'b1;
end
initial
begin
#180 $stop;
end
endmodule
|
The above code is simulated in Modelsim and below are the simulated result:
The above result shows the correct working of the Full adder as provided in the truth table.
These two examples are the basic guidelines on how to write code in a hierarchical style.









沒有留言:
張貼留言