C語言二分法 Program for Bisection Method

C語言二分法
源自於 https://www.geeksforgeeks.org/program-for-bisection-method/

Program for Bisection Method

Given a function f(x) on floating number x and two numbers ‘a’ and ‘b’ such that f(a)*f(b) < 0 and f(x) is continuous in [a, b]. Here f(x) represents algebraic or transcendental equation. Find root of function in interval [a, b] (Or find a value of x such that f(x) is 0).
Example:

Input: A function of x, for example x3 - x2 + 2.     
       And two values: a = -200 and b = 300 such that
       f(a)*f(b) < 0, i.e., f(a) and f(b) have
       opposite signs.
Output: The value of root is : -1.0025
        OR any other value with allowed
        deviation from root.

What are Algebraic and Transcendental functions?
Algebraic function are the one which can be represented in the form of polynomials like f(x) = a1x3 + a2x2 + ….. + e where aa1, a2, … are constants and x is a variable.
Transcendental function are non algebraic functions, for example f(x) = sin(x)*x – 3 or f(x) = ex + x2 or f(x) = ln(x) + x ….

What is Bisection Method?
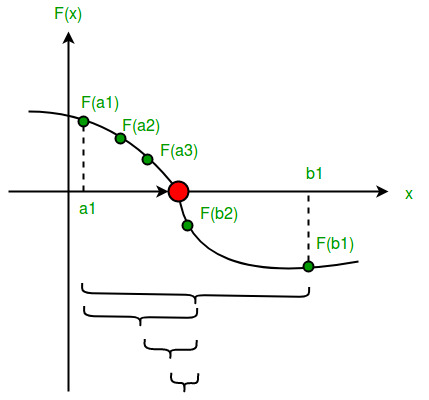
The method is also called the interval halving method, the binary search method or the dichotomy method. This method is used to find root of an equation in a given interval that is value of ‘x’ for which f(x) = 0 .

The method is based on The Intermediate Value Theorem which states that if f(x) is a continuous function and there are two real numbers a and b such that f(a)*f(b) 0 and f(b) < 0), then it is guaranteed that it has at least one root between them.

Assumptions:

1. f(x) is a continuous function in interval [a, b]
2. f(a) * f(b) < 0

Steps:

1. Find middle point c= (a + b)/2 .
2. If f(c) == 0, then c is the root of the solution.
3. Else f(c) != 0
   1. If value f(a)*f(c) < 0 then root lies between a and c. So we recur for a and c
   2. Else If f(b)*f(c) < 0 then root lies between b and c. So we recur b and c.
   3. Else given function doesn’t follow one of assumptions.

Since root may be a floating point number, we repeat above steps while difference between a and b is less than a value ? (A very small value).

Below is implementation of above steps

程式 : 

// C program for implementation of Bisection Method for 
// solving equations 
#include <stdio.h>
#define EPSILON 0.01 
  
// An example function whose solution is determined using 
// Bisection Method. The function is x^3 - x^2  + 2 
double func(double x) 
{ 
    return x*x*x - x*x + 2; 
} 
  
// Prints root of func(x) with error of EPSILON 
void bisection(double a, double b) 
{ 
    if (func(a) * func(b) >= 0) 
    { 
        printf("You have not assumed right a and b\n"); 
        return; 
    } 
  
    double c = a; 
    while ((b-a) >= EPSILON) 
    { 
        // Find middle point 
        c = (a+b)/2; 
  
        // Check if middle point is root 
        if (func(c) == 0.0) 
            break; 
  
        // Decide the side to repeat the steps 
        else if (func(c)*func(a) < 0) 
            b = c; 
        else
            a = c; 
    } 
    printf("The value of root is :%.4lf\n" ,c); 
} 
  
// Driver program to test above function 
int main() 
{ 
    // Initial values assumed 
    double a =-200, b = 300; 
    bisection(a, b); 
    return 0; 
} 

The value of root is : -1.0025