C語言 例題2-3 已知非線性方程式 x^3 + 4x^2 -10 =0 請使用Newton-Raphson方法找出其位於(1.0,2.0)之間的根=?

C語言Newton-Raphson方法求非線性方程式的解
例題2-3 已知非線性方程式
x^3 + 4x^2 -10 =0
請使用Newton-Raphson方法找出其位於(1.0,2.0)之間的根=?

源自於https://www.geeksforgeeks.org/program-for-newton-raphson-method/

程式

// C program for implementation of Newton Raphson Method for 
// solving equations 

#include <stdio.h>
#include <math.h>

#define EPSILON 0.001 

// An example function whose solution is determined using 
// Bisection Method. The function is x^3 + 4x^2  - 10 
double func(double x) 
{ 
    return x*x*x + 4*x*x - 10; 
} 
  
// Derivative of the above function which is 3*x^x + 8*x 
double derivFunc(double x) 
{ 
    return 3*x*x + 8*x; 
} 
  
// Function to find the root 
void newtonRaphson(double x) 
{ 
    double h = func(x) / derivFunc(x); 
    int i=0;
    while (abs(h) >= EPSILON) 
    { 
        h = func(x)/derivFunc(x); 
   
        // x(i+1) = x(i) - f(x) / f'(x)   
        x = x - h; 
        i+=1;
        if (i>=1000)
           break;
    } 
  
    printf("The value of the root is : %0.6lf ", x); 
} 
  
// Driver program to test above 
int main() 
{ 
    double x0 = 1.0; // Initial values assumed 
    newtonRaphson(x0); 
    return 0; 
} 

The value of the root is : 1.365230                                                                                                                                                              
                                                                                                                                                                                                 
...Program finished with exit code 0                                                                                                                                                             
Press ENTER to exit console.                                                                                                                                                                     
                                

Program for Newton Raphson Method

Given a function f(x) on floating number x and an initial guess for root, find root of function in interval. Here f(x) represents algebraic or transcendental equation.

For simplicity, we have assumed that derivative of function is also provided as input.

Example:

Input: A function of x (for example x3 – x2 + 2),
       derivative function of x (3x2 – 2x for above example)
       and an initial guess x0 = -20
Output: The value of root is : -1.00
        OR any other value close to root.

We have discussed below methods to find root in set 1 and set 2
Set 1: The Bisection Method
Set 2: The Method Of False Position

Comparison with above two methods:

1. In previous methods, we were given an interval. Here we are required an initial guess value of root.
2. The previous two methods are guaranteed to converge, Newton Rahhson may not converge in some cases.
3. Newton Raphson method requires derivative. Some functions may be difficult to
   impossible to differentiate.
4. For many problems, Newton Raphson method converges faster than the above two methods.
5. Also, it can identify repeated roots, since it does not look for changes in the sign of f(x) explicitly

The formula:
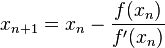
Starting from initial guess x1, the Newton Raphson method uses below formula to find next value of x, i.e., xn+1 from previous value xn.

Algorithm:
Input: initial x, func(x), derivFunc(x)
Output: Root of Func()

1. Compute values of func(x) and derivFunc(x) for given initial x
2. Compute h: h = func(x) / derivFunc(x)
3. While h is greater than allowed error ε
   1. h = func(x) / derivFunc(x)
   2. x = x – h

Below is the implementation of above algorithm.

How does this work?
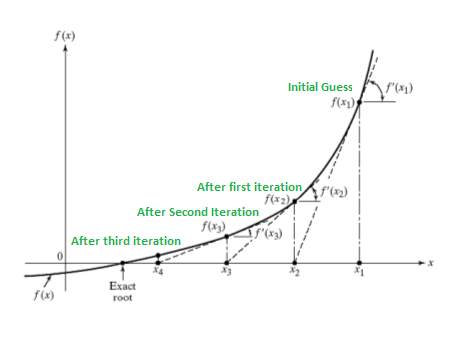
The idea is to draw a line tangent to f(x) at point x1. The point where the tangent line crosses the x axis should be a better estimate of the root than x1. Call this point x2. Calculate f(x2), and draw a line tangent at x2.

We know that slope of line from (x1, f(x1)) to (x2, 0) is f'(x1)) where f’ represents derivative of f.

f'(x1) = (0 - f(x1)) / (x2 - x1) 

f'(x1) *  (x2 - x1) =  - f(x1)

x2 =  x1 - f(x1) / f'(x1) 

By finding this point 'x2', we move closer towards the root.
We have to keep on repeating the above step till we we get really close to 
the root or we find it.

In general, 
xn+1 =  xn - f(xn) / f'(xn) 

Alternate Explanation using Taylor’s Series:

Let x1 be the initial guess. 

We can write x2 as below:
  xn+1  = xn + h ------- (1)
Here h would be a small value that can be positive or negative.

According to Taylor's Series, 
ƒ(x) that is infinitely differentiable can be written as below
f(xn+1) = f(xn  + h) 
       = f(xn) + h*f'(xn) + ((h*h)/2!)*(f''(xn)) + ...

Since we are looking for root of function, f(xn+1) = 0

f(xn) + h*f'(xn) + ((h*h)/2!)*(f''(xn)) + ... = 0

Now since h is small, h*h would be very small. 
So if we ignore higher order terms, we get

f(xn) + h*f'(xn) = 0

Substituting this value of h = xn+1 - xn from equation (1) we get, 
f(xn) + (xn+1  - xn)*f'(xn) = 0

xn+1 =  xn - f(xn) / f'(xn)  

Notes:

1. We generally used this method to improve the result obtained by either bisection method or method of false position.
2. Babylonian method for square root is derived from the Newton-Raphson method.