Program for Gauss-Jordan Elimination Method
Input : 2y + z = 4
x + y + 2z = 6
2x + y + z = 7
Explanation : Below given is the explanation of the above example.
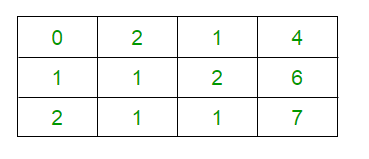
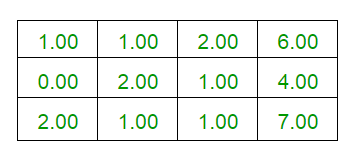
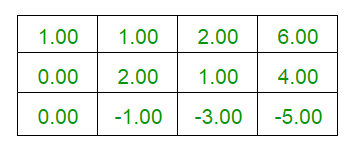
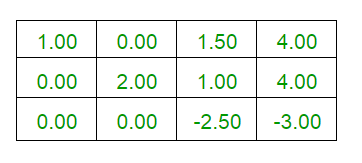

/*
Input : 2y + z = 4
x + y + 2z = 6
2x + y + z = 7
*/
// C Implementation for Gauss-Jordan Elimination Method
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define M 10
// Function to print the matrix
void PrintMatrix(float a[][M], int n)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j <= n; j++)
printf("%4.3lf ", a[i][j]);
printf("\n");
}
}
// function to reduce matrix to reduced
// row echelon form.
int PerformOperation(float a[][M], int n)
{
int i, j, k = 0, c, flag = 0, m = 0;
float pro = 0;
// Performing elementary operations
for (i = 0; i < n; i++)
{
if (a[i][i] == 0)
{
c = 1;
while (a[i + c][i] == 0 && (i + c) < n)
c++;
if ((i + c) == n) {
flag = 1;
break;
}
for (j = i, k = 0; k <= n; k++)
{
float tmp= a[j+c][k];
a[j+c][k]=a[j][k];
a[j][k]=tmp;
//printf("%3.4lf ",a[j][k] );
//swap(a[j][k], a[j+c][k]);
}
//printf("\n\n");
}
for (j = 0; j < n; j++) {
// Excluding all i == j
if (i != j) {
// Converting Matrix to reduced row
// echelon form(diagonal matrix)
float pro = a[j][i] / a[i][i];
for (k = 0; k <= n; k++)
{
a[j][k] = a[j][k] - (a[i][k]) * pro;
//printf("%3.4lf ",a[j][k] );
}
//printf("\n\n");
}
}
}
return flag;
}
// Function to print the desired result
// if unique solutions exists, otherwise
// prints no solution or infinite solutions
// depending upon the input given.
void PrintResult(float a[][M], int n, int flag)
{
printf("Result is : ");
if (flag == 2)
printf("Infinite Solutions Exists");
else if (flag == 3)
printf("No Solution Exists");
// Printing the solution by dividing constants by
// their respective diagonal elements
else {
for (int i = 0; i < n; i++)
printf("\nx[%d]=%0.2lf" , i, (a[i][n] / a[i][i]) );
}
}
// To check whether infinite solutions
// exists or no solution exists
int CheckConsistency(float a[][M], int n, int flag)
{
int i, j;
float sum;
// flag == 2 for infinite solution
// flag == 3 for No solution
flag = 3;
for (i = 0; i < n; i++)
{
sum = 0;
for (j = 0; j < n; j++)
sum = sum + a[i][j];
if (sum == a[i][j])
flag = 2;
}
return flag;
}
// Driver code
int main()
{
float a[M][M] = {{ 0, 2, 1, 4 },
{ 1, 1, 2, 6 },
{ 2, 1, 1, 7 }};
// Order of Matrix(n)
int n = 3, flag = 0;
printf("Orginal Augumented Matrix is :\n ");
PrintMatrix(a, n);
// Performing Matrix transformation
flag = PerformOperation(a, n);
if (flag == 1)
flag = CheckConsistency(a, n, flag);
// Printing Final Matrix
printf("\nFinal Augumented Matrix is : \n");
PrintMatrix(a, n);
printf("\n");
// Printing Solutions(if exist)
PrintResult(a, n, flag);
return 0;
}
輸出畫面
Orginal Augumented Matrix is :
0.000 2.000 1.000 4.000
1.000 1.000 2.000 6.000
2.000 1.000 1.000 7.000
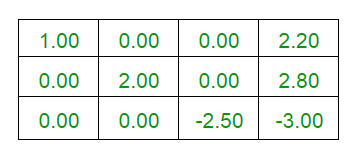
Final Augumented Matrix is :
1.000 0.000 0.000 2.200
0.000 2.000 0.000 2.800
0.000 0.000 -2.500 -3.000
Result is :
x[0]=2.20
x[1]=1.40
x[2]=1.20


沒有留言:
張貼留言