NEWTON’S GREGORY FORWARD INTERPOLATION FORMULA :

NEWTON’S GREGORY FORWARD INTERPOLATION FORMULA :

This formula is particularly useful for interpolating the values of f(x) near the beginning of the set of values given. h is called the interval of difference and u = ( x – a ) / h, Here a is first term.

Example :

Input : Value of Sin 52
  
Output :

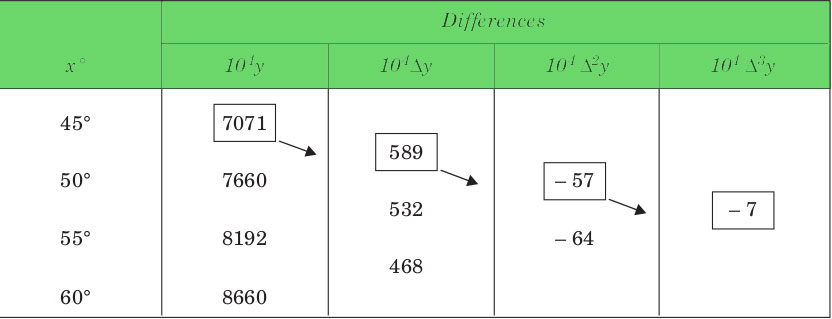Value at Sin 52 is 0.788003

Below is the implementation of newton forward interpolation method.

// CPP Program to interpolate using  // newton forward interpolation #include <bits/stdc++.h> using namespace std;    // calculating u mentioned in the formula float u_cal(float u, int n) {     float temp = u;     for (int i = 1; i < n; i++)         temp = temp * (u - i);     return temp; }    // calculating factorial of given number n int fact(int n) {     int f = 1;     for (int i = 2; i <= n; i++)         f *= i;     return f; }    int main() {     // Number of values given     int n = 4;     float x[] = { 45, 50, 55, 60 };            // y[][] is used for difference table     // with y[][0] used for input     float y[n][n];     y[0][0] = 0.7071;     y[1][0] = 0.7660;     y[2][0] = 0.8192;     y[3][0] = 0.8660;        // Calculating the forward difference     // table     for (int i = 1; i < n; i++) {         for (int j = 0; j < n - i; j++)             y[j][i] = y[j + 1][i - 1] - y[j][i - 1];     }        // Displaying the forward difference table     for (int i = 0; i < n; i++) {         cout << setw(4) << x[i]               << "\t";         for (int j = 0; j < n - i; j++)             cout << setw(4) << y[i][j]                   << "\t";         cout << endl;     }        // Value to interpolate at     float value = 52;        // initializing u and sum     float sum = y[0][0];     float u = (value - x[0]) / (x[1] - x[0]);     for (int i = 1; i < n; i++) {         sum = sum + (u_cal(u, i) * y[0][i]) /                                  fact(i);     }        cout << "\n Value at " << value << " is "           << sum << endl;     return 0; }

Output:

  45    0.7071    0.0589    -0.00569999    -0.000699997    
  50    0.766    0.0532    -0.00639999    
  55    0.8192    0.0468    
  60    0.866    

  Value at 52 is 0.788003