Lagrange’s Interpolation
源自於 https://www.geeksforgeeks.org/lagranges-interpolation/
// C++ program for implementation of Lagrange's Interpolation
#include<bits/stdc++.h>
using namespace std;
// To represent a data point corresponding to x and y = f(x)
struct Data
{
int x, y;
};
// function to interpolate the given data points using Lagrange's formula
// xi corresponds to the new data point whose value is to be obtained
// n represents the number of known data points
double interpolate(Data f[], int xi, int n)
{
double result = 0; // Initialize result
for (int i=0; i<n; i++)
{
// Compute individual terms of above formula
double term = f[i].y;
for (int j=0;j<n;j++)
{
if (j!=i)
term = term*(xi - f[j].x)/double(f[i].x - f[j].x);
}
// Add current term to result
result += term;
}
return result;
}
// driver function to check the program
int main()
{
// creating an array of 4 known data points
Data f[] = {{0,2}, {1,3}, {2,12}, {5,147}};
// Using the interpolate function to obtain a data point
// corresponding to x=3
cout << "Value of f(3) is : " << interpolate(f, 3, 4);
return 0;
}
Lagrange’s Interpolation
What is Interpolation?
Interpolation is a method of finding new data points within the range of a discrete set of known data points (Source Wiki). In other words interpolation is the technique to estimate the value of a mathematical function, for any intermediate value of the independent variable.
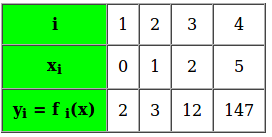
For example, in the given table we’re given 4 set of discrete data points, for an unknown function f(x) :
Interpolation is a method of finding new data points within the range of a discrete set of known data points (Source Wiki). In other words interpolation is the technique to estimate the value of a mathematical function, for any intermediate value of the independent variable.
For example, in the given table we’re given 4 set of discrete data points, for an unknown function f(x) :
How to find?
Here we can apply the Lagrange’s interpolation formula to get our solution.
The Lagrange’s Interpolation formula:
If, y = f(x) takes the values y0, y1, … , yn corresponding to x = x0, x1 , … , xn then,
Here we can apply the Lagrange’s interpolation formula to get our solution.
The Lagrange’s Interpolation formula:
If, y = f(x) takes the values y0, y1, … , yn corresponding to x = x0, x1 , … , xn then,
This method is preferred over its counterparts like Newton’s method because it is applicable even for unequally spaced values of x.
We can use interpolation techniques to find an intermediate data point say at x = 3.
Output:
Value of f(3) is : 35
Complexity:
The time complexity of the above solution is O(n2) and auxiliary space is O(1).
The time complexity of the above solution is O(n2) and auxiliary space is O(1).






沒有留言:
張貼留言