|
源自於 http://www.stat.nuk.edu.tw/cbme/math/calculus/cal2/c6_4/bud.htm
定積分之數值計算
在實際應用時, 可取
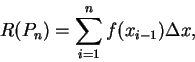 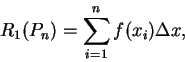 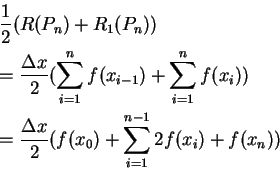 。 。
設
其次來看梯形法之一推廣, 此法源自於 Simpson (1710-1761), 故稱之為 Simpson 法 (Simpson's rule), 為一較梯形法更精確的估計定積分的方法。
設
通過此三點, 其中係數
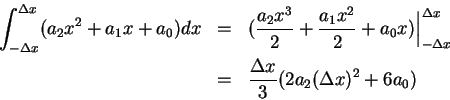 。 。
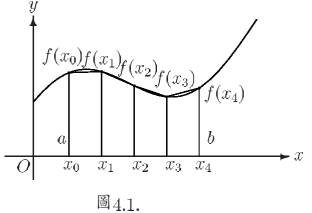
此即圖 4.2 中拋物線下的面積。
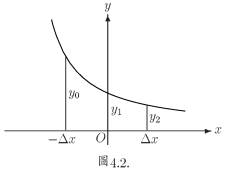
若將拋物線平移, 設有一拋物線
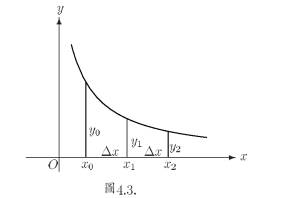
設
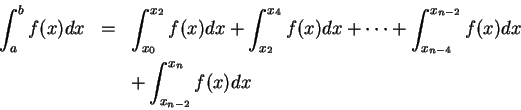 。 。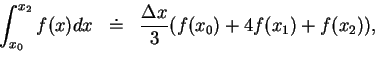 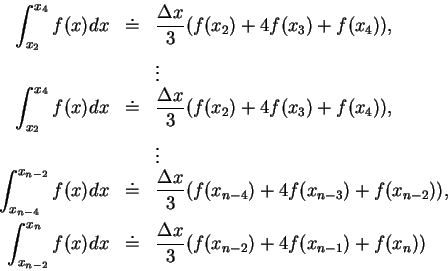 。 。
即 Simpson 法對積分之逼近。
| ||||||||||||||||||||||
2018年12月31日 星期一
定積分之數值計算
訂閱:
張貼留言 (Atom)
ESP32 (ESP-IDF in VS Code) MFRC522 + MQTT + PYTHON TKinter +SQLite
ESP32 (ESP-IDF in VS Code) MFRC522 + MQTT + PYTHON TKinter +SQLite ESP32 VS Code 程式 ; PlatformIO Project Configuration File ; ; Build op...

-
python pip 不是内部或外部命令 -- 解決方法 要安裝 Pyqt5 1. 首先,開啟命令提示字元。 2. 輸入 pip3 install pyqt5 好像不能執行 ! ! 錯誤顯示 : ‘ pip3 ’ 不是內部或外部命令、可執行的程式或批...
-
課程講義 下載 11/20 1) PPT 下載 + 程式下載 http://www.mediafire.com/file/cru4py7e8pptfda/106%E5%8B%A4%E7%9B%8A2-1.rar 11/27 2) PPT 下載...
-
• 認 識 PreFix、InFix、PostFix PreFix(前序式):* + 1 2 + 3 4 InFix(中序式): (1+2)*(3+4) PostFix(後序式):1 2 + 3 4 + * 後 序式的運算 例如: 運算時由 後序式的...
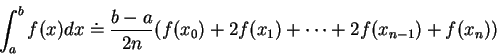 。
。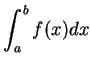
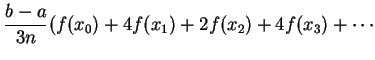

沒有留言:
張貼留言