Newton’s Divided Difference Interpolation Formula
Interpolation is an estimation of a value within two known values in a sequence of values.
Newton’s divided difference interpolation formula is a interpolation technique used when the interval difference is not same for all sequence of values.
Suppose f(x0), f(x1), f(x2)………f(xn) be the (n+1) values of the function y=f(x) corresponding to the arguments x=x0, x1, x2…xn, where interval differences are not same
Then the first divided difference is given by
Then the first divided difference is given by
The second divided difference is given by
and so on…
Divided differences are symmetric with respect to the arguments i.e independent of the order of arguments.
so,
f[x0, x1]=f[x1, x0]
f[x0, x1, x2]=f[x2, x1, x0]=f[x1, x2, x0]
By using first divided difference, second divided difference as so on .A table is formed which is called the divided difference table.
Divided differences are symmetric with respect to the arguments i.e independent of the order of arguments.
so,
f[x0, x1]=f[x1, x0]
f[x0, x1, x2]=f[x2, x1, x0]=f[x1, x2, x0]
By using first divided difference, second divided difference as so on .A table is formed which is called the divided difference table.
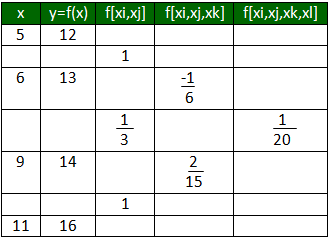
Divided difference table:


NEWTON’S DIVIDED DIFFERENCE INTERPOLATION FORMULA
Examples:
Input : Value at 7
 Output :
Output :
 Value at 7 is 13.47
Value at 7 is 13.47
Recommended: Please try your approach on {IDE} first, before moving on to the solution.
// CPP program for implementing
// Newton divided difference formula
#include <bits/stdc++.h>
using namespace std;
// Function to find the product term
float proterm(int i, float value, float x[])
{
float pro = 1;
for (int j = 0; j < i; j++) {
pro = pro * (value - x[j]);
}
return pro;
}
// Function for calculating
// divided difference table
void dividedDiffTable(float x[], float y[][10], int n)
{
for (int i = 1; i < n; i++) {
for (int j = 0; j < n - i; j++) {
y[j][i] = (y[j][i - 1] - y[j + 1]
[i - 1]) / (x[j] - x[i + j]);
}
}
}
// Function for applying Newton's
// divided difference formula
float applyFormula(float value, float x[],
float y[][10], int n)
{
float sum = y[0][0];
for (int i = 1; i < n; i++) {
sum = sum + (proterm(i, value, x) * y[0][i]);
}
return sum;
}
// Function for displaying
// divided difference table
void printDiffTable(float y[][10],int n)
{
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - i; j++) {
cout << setprecision(4) <<
y[i][j] << "\t ";
}
cout << "\n";
}
}
// Driver Function
int main()
{
// number of inputs given
int n = 4;
float value, sum, y[10][10];
float x[] = { 5, 6, 9, 11 };
// y[][] is used for divided difference
// table where y[][0] is used for input
y[0][0] = 12;
y[1][0] = 13;
y[2][0] = 14;
y[3][0] = 16;
// calculating divided difference table
dividedDiffTable(x, y, n);
// displaying divided difference table
printDiffTable(y,n);
// value to be interpolated
value = 7;
// printing the value
cout << "\nValue at " << value << " is "
<< applyFormula(value, x, y, n) << endl;
return 0;
}
Output:
12 1 -0.1667 0.05 13 0.3333 0.1333 14 1 16 Value at 7 is 13.47
12 1 -0.1667 0.05
13 0.3333 0.1333
14 1
16
Value at 7 is 13.47
...Program finished with exit code 0
Press ENTER to exit console.




沒有留言:
張貼留言