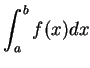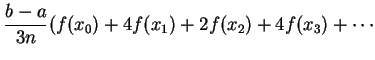源自於
https://www.geeksforgeeks.org/program-simpsons-13-rule/
In numerical analysis, Simpson’s 1/3 rule is a method for numerical approximation of definite integrals. Specifically, it is the following approximation:
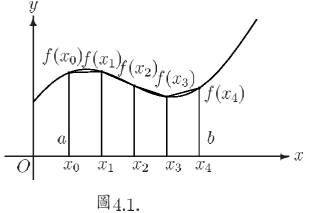
In Simpson’s 1/3 Rule, we use parabolas to approximate each part of the curve.We divide
the area into n equal segments of width Δx.
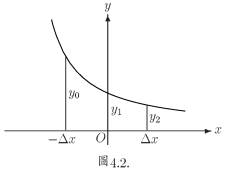
Simpson’s rule can be derived by approximating the integrand f (x) (in blue)
by the quadratic interpolant P(x) (in red).

the area into n equal segments of width Δx.
Simpson’s rule can be derived by approximating the integrand f (x) (in blue)
by the quadratic interpolant P(x) (in red).

In order to integrate any function f(x) in the interval (a, b), follow the steps given below:
1.Select a value for n, which is the number of parts the interval is divided into.
2.Calculate the width, h = (b-a)/n
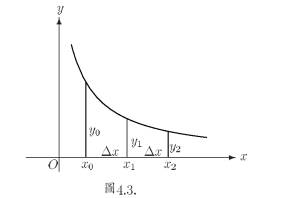
3.Calculate the values of x0 to xn as x0 = a, x1 = x0 + h, …..xn-1 = xn-2 + h, xn = b.
Consider y = f(x). Now find the values of y(y0 to yn) for the corresponding x(x0 to xn) values.
4.Substitute all the above found values in the Simpson’s Rule Formula to calculate the integral value.
2.Calculate the width, h = (b-a)/n
3.Calculate the values of x0 to xn as x0 = a, x1 = x0 + h, …..xn-1 = xn-2 + h, xn = b.
Consider y = f(x). Now find the values of y(y0 to yn) for the corresponding x(x0 to xn) values.
4.Substitute all the above found values in the Simpson’s Rule Formula to calculate the integral value.
Approximate value of the integral can be given by Simpson’s Rule:
Note : In this rule, n must be EVEN.
Application :
It is used when it is very difficult to solve the given integral mathematically.
This rule gives approximation easily without actually knowing the integration rules.
It is used when it is very difficult to solve the given integral mathematically.
This rule gives approximation easily without actually knowing the integration rules.
Example :
Evaluate logx dx within limit 4 to 5.2.
First we will divide interval into six equal
parts as number of interval should be even.
x : 4 4.2 4.4 4.6 4.8 5.0 5.2
logx : 1.38 1.43 1.48 1.52 1.56 1.60 1.64
Now we can calculate approximate value of integral
using above formula:
= h/3[( 1.38 + 1.64) + 4 * (1.43 + 1.52 +
1.60 ) +2 *(1.48 + 1.56)]
= 1.84
Hence the approximation of above integral is
1.827 using Simpson's 1/3 rule.
// CPP program for simpson's 1/3 rule #include <iostream> #include <math.h> using namespace std; // Function to calculate f(x) float func(float x) { return log(x); } // Function for approximate integral float simpsons_(float ll, float ul, int n) { // Calculating the value of h float h = (ul - ll) / n; // Array for storing value of x and f(x) float x[10], fx[10]; // Calculating values of x and f(x) for (int i = 0; i <= n; i++) { x[i] = ll + i * h; fx[i] = func(x[i]); } // Calculating result float res = 0; for (int i = 0; i <= n; i++) { if (i == 0 || i == n) res += fx[i]; else if (i % 2 != 0) res += 4 * fx[i]; else res += 2 * fx[i]; } res = res * (h / 3); return res; } // Driver program int main() { float lower_limit = 4; // Lower limit float upper_limit = 5.2; // Upper limit int n = 6; // Number of interval cout << simpsons_(lower_limit, upper_limit, n); return 0; }
Output:
1.827847
Python 語言
# Python code for simpson's 1 / 3 rule import math # Function to calculate f(x) def func( x ): return math.log(x) # Function for approximate integral def simpsons_( ll, ul, n ): # Calculating the value of h h = ( ul - ll )/n # List for storing value of x and f(x) x = list() fx = list() # Calcuting values of x and f(x) i = 0 while i<= n: x.append(ll + i * h) fx.append(func(x[i])) i += 1 # Calculating result res = 0 i = 0 while i<= n: if i == 0 or i == n: res+= fx[i] elif i % 2 != 0: res+= 4 * fx[i] else: res+= 2 * fx[i] i+= 1 res = res * (h / 3) return res # Driver code lower_limit = 4 # Lower limit upper_limit = 5.2 # Upper limit n = 6 # Number of interval print("%.6f"% simpsons_(lower_limit, upper_limit, n))


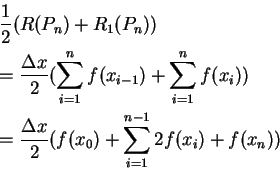 。
。 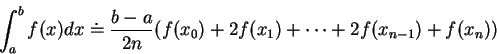 。
。
 。
。
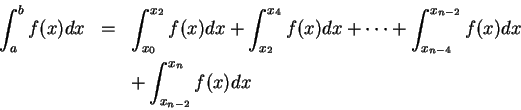 。
。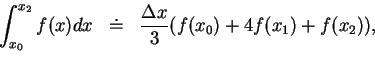
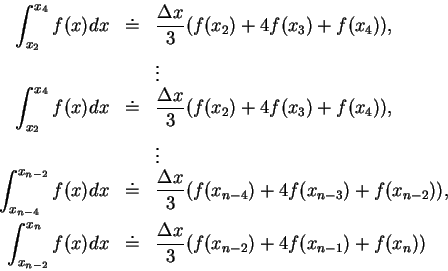 。
。