曼徹斯特編碼 (Manchester Encoding) ---python

 曼徹斯特編碼 

曼徹斯特編碼   參考來源 https://www.cs.nthu.edu.tw/~nfhuang/chap02.htm

曼徹斯特編碼 (Manchester Encoding) 是許多區域網路採用的編碼技巧。其主要特性是無論資料是 0 或 1，在每一個位元時間的中央都有電位的轉換。由正電位到負電位代表 "0"，而由負電位到正電位則代表 "1"，如圖2-14 所示。

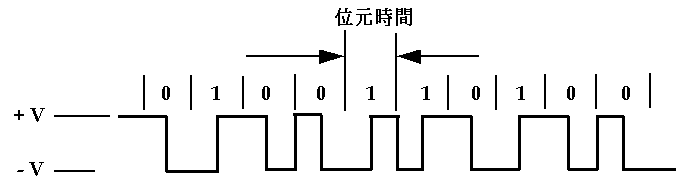
圖2-14 曼徹斯特編碼範例

　

此特性的主要目的是讓資料傳送端與接收端在資料傳送及接收時達到同步(synchronization) 的效果。由於區域網路上所傳送的資料較長（如IEEE 802.3 CSMA/CD 網路每一筆資料可長達 1518 位元組，IEEE 802.4 Token-bus 網路每一筆資料可長達 8191 位元組等等），當資料內容出現一長串相同的值時（如一連串的 "1" 或一連串的 "0"）常會造成接收端在接收資料的錯誤。假設資料編碼技巧為 Zero-complemented 差動式編碼，則對於一長串連續為 "1" 的資料來說，傳輸線上會出現好一陣子沒有變化的電位，其時間 t＝位元時間×位元個數。在接收端方面，通常使用自己的時序 (clock) 到傳輸線上以取樣 (sampling) 的方式讀取資炓，如圖2-15 所示。

　

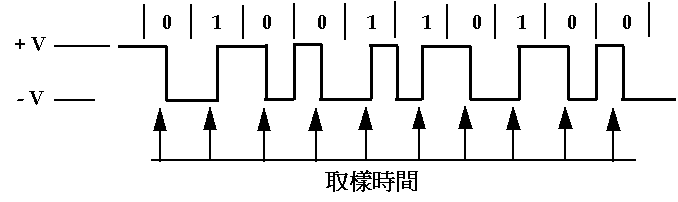
圖2-15 接收端讀取資料時間

在傳送速率與接收速率完全相同時，接收端的取樣動作便不會發生問題。如果有一點差異，則容易造成在取樣時的時間差（或稱相位差），這種時間差會在每個位元時間中慢慢累積，最後可能導致取樣時發生錯誤。也就是說，如果傳輸線上無論其值為何而能一直有電位變化的話則可以給接收端一個參考的取樣時間，使其能達到「同步」取樣的功效。當傳輸速率越快時，每一個位元時間便越短，例如傳輸速率為 10 Mbps，則每一個位元時間為

1/10×10⁶ ＝ 10^-7 s ＝ 100ns。

如果沒有同步的功能則會使得取樣時越容易發生錯誤。

IEEE 802.3 CSMA/CD 網路便採用了曼徹斯特編碼技術。

import tkinter as tk

from tkinter import ttk, messagebox

# --- 曼徹斯特編碼邏輯 ---

def manchester_encode(data_bit):

    """

    根據曼徹斯特編碼規則，將單一資料位元轉換為波形電位序列。

    規則：

    '0'：正電位 -> 負電位 (High -> Low)

    '1'：負電位 -> 正電位 (Low -> High)

    """

    if data_bit == '0':

        # (高, 低)

        return (1, -1)

    elif data_bit == '1':

        # (低, 高)

        return (-1, 1)

    else:

        # 處理無效輸入

        return (0, 0)

# --- 繪圖函式 ---

def draw_manchester_waveform(canvas, binary_data):

    """

    在 Tkinter Canvas 上繪製曼徹斯特編碼波形。

    """

    # 清空畫布

    canvas.delete("all")

    # 設定基本參數

    WIDTH = 600

    HEIGHT = 200

    canvas.config(width=WIDTH, height=HEIGHT)

    NUM_BITS = len(binary_data)

    

    if NUM_BITS == 0:

        return

    # 定義座標和比例尺

    BIT_WIDTH = WIDTH // NUM_BITS  # 每個位元佔用的水平空間

    MID_HEIGHT = HEIGHT // 2       # 零電位線

    AMPLITUDE = MID_HEIGHT - 20    # 振幅 (電位高度)

    

    # 繪製零電位線 (基準線) - 修改為深藍色

    canvas.create_line(0, MID_HEIGHT, WIDTH, MID_HEIGHT, fill="darkblue", dash=(4, 2))

    canvas.create_text(20, MID_HEIGHT + 15, text="0V (基準)", fill="darkblue") # 標記文字也改為深藍色

    

    # 繪製高/低電位標記

    canvas.create_text(20, MID_HEIGHT - AMPLITUDE - 10, text="+V", fill="red")

    canvas.create_text(20, MID_HEIGHT + AMPLITUDE + 10, text="-V", fill="red")

    

    # 用於儲存波形點的列表

    waveform_points_coords = []

    

    # 繪製資料位元標記及生成波形點

    for i in range(NUM_BITS):

        x_start = i * BIT_WIDTH

        x_end = (i + 1) * BIT_WIDTH

        x_mid = x_start + BIT_WIDTH // 2

        

        # 繪製位元間的垂直虛線 - 修改為深藍色

        if i < NUM_BITS:

            canvas.create_line(x_end, 0, x_end, HEIGHT, fill="darkblue", dash=(2, 2))

        

        # 標記資料位元

        canvas.create_text(x_start + BIT_WIDTH/2, 10, 

                           text=binary_data[i], fill="blue", font=('Arial', 10, 'bold'))

        # 進行編碼

        data_bit = binary_data[i]

        encoded_levels = manchester_encode(data_bit)

        

        # 將電位轉換為 Canvas 座標

        def get_y_coord(level):

            if level == 1:    # +V

                return MID_HEIGHT - AMPLITUDE

            elif level == -1: # -V

                return MID_HEIGHT + AMPLITUDE

            else:             # 0V (應該不會發生)

                return MID_HEIGHT

        

        y1 = get_y_coord(encoded_levels[0])

        y2 = get_y_coord(encoded_levels[1])

        

        # 加入此位元的波形點

        # 1. 位元起始點

        if i == 0: # 只有第一個位元才加入最左邊的起始點

            waveform_points_coords.append((x_start, y1))

        elif i > 0 and waveform_points_coords:

            # 如果是前一個位元的結束點和當前位元起始點Y值不同，則需要先畫垂直線連接

            prev_x_end, prev_y_end = waveform_points_coords[-1]

            if prev_y_end != y1:

                canvas.create_line(x_start, prev_y_end, x_start, y1, fill="red", width=3)

            # 因為前面已經處理了連接，這裡只需要確保起始點是正確的

            waveform_points_coords.append((x_start, y1))

        # 2. 中間點 (第一個半位元水平線結束)

        waveform_points_coords.append((x_mid, y1))

        

        # 3. 中央轉換點 (垂直線結束，第二半位元水平線開始)

        waveform_points_coords.append((x_mid, y2))

        

        # 4. 位元結束點

        waveform_points_coords.append((x_end, y2))

    

    # 繪製最終波形

    for i in range(len(waveform_points_coords) - 1):

        x1, y1 = waveform_points_coords[i]

        x2, y2 = waveform_points_coords[i+1]

        canvas.create_line(x1, y1, x2, y2, fill="red", width=3)

# --- 應用程式主體 ---

def main():

    root = tk.Tk()

    root.title("曼徹斯特編碼波形產生器 (含連續 '1' 錯誤檢測)")

    # --- 1. 輸入框和按鈕區域 ---

    input_frame = ttk.Frame(root, padding="10")

    input_frame.pack(fill='x', padx=10, pady=10)

    ttk.Label(input_frame, text="輸入 10 位二進制資料 (0或1)：").pack(side='left', padx=(0, 10))

    data_entry = ttk.Entry(input_frame, width=15)

    data_entry.pack(side='left', padx=(0, 10))

    # 預設輸入 (正常)

    data_entry.insert(0, "1011001010") 

    def visualize():

        binary_data = data_entry.get()

        

        # 1. 驗證長度

        if len(binary_data) != 10:

            messagebox.showerror("輸入錯誤", "請輸入剛好 10 位的二進制資料。")

            return

        

        # 2. 驗證內容

        if not all(c in '01' for c in binary_data):

            messagebox.showerror("輸入錯誤", "資料必須只包含 '0' 或 '1'。")

            return

        

        # 3. 檢查「連續 11 個 '1'」錯誤 (雖然這裡只有 10 位，我們可以修改條件來模擬)

        # 在此範例中，由於只有 10 位，我們設定為「連續 5 個 '1'」來觸發錯誤

        if "11111" in binary_data: # 這裡改為偵測連續 5 個 '1'

            messagebox.showwarning("通訊錯誤！", "偵測到連續 '1' (類似 '連續 11 時錯誤')，通訊可能中斷！")

            

        draw_manchester_waveform(canvas, binary_data)

    visualize_button = ttk.Button(input_frame, text="生成波形", command=visualize)

    visualize_button.pack(side='left')

    # --- 2. 繪圖畫布區域 ---

    canvas_frame = ttk.Frame(root, padding="10")

    canvas_frame.pack(fill='both', expand=True, padx=10, pady=5)

    

    # 創建 Canvas

    canvas = tk.Canvas(canvas_frame, bg="white", width=600, height=200, borderwidth=1, relief="solid")

    canvas.pack(fill='both', expand=True)

    

    # 初始化繪圖

    visualize()

    root.mainloop()

if __name__ == "__main__":

    main()