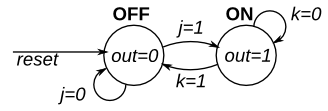
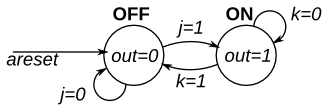
HDLBits FSM/Design a Moore FSM (Exams/ece241 2013 q4)
題目內容翻譯:
大型水庫可為多個用戶提供服務。為了使水位足夠高,三個傳感器以5英寸的間隔垂直放置。當水位高於最高傳感器(S3)時,輸入流量應為零。當液位低於最低傳感器(S1)時,流量應最大(標稱流量閥和輔助流量閥均打開)。當水位在上下傳感器之間時,流速由兩個因素決定:水位和最後一個傳感器變化之前的水位。每種水位都有一個與之相關的標稱流速,如下表所示。如果傳感器變化表明先前的液位低於當前的液位,則應進行標稱流速。如果先前的水平高於當前水平,則應通過打開輔助流量閥(由ΔFR控制)來增加流量。
繪制水庫控制器的摩爾模型狀態圖。清楚地指出每個狀態的所有狀態轉換和輸出。 FSM的輸入為S1,S2和S3。輸出為FR1,FR2,FR3和ΔFR。
把四個水閥的狀態合並成一個四位二進制,
根據題目中的提供的信息,可以得到下面圖中的水閥狀態一共是有S0-S7一共8種,但是S1和S6實際上是不存在的狀態,從狀態跳轉圖也可以很清楚看出來是不穩定的。
最主要的是輔助流量閥ΔFR的值,這里需要注意的是,如果水位從4變到5,即其依舊保持在S2與S3之間,這個時候表示傳感器其實是沒有探測到水位變化的,所以說ΔFR的值是並不會變化的。
具體的水閥開關和狀態跳轉在下圖中給了明確表示,為了避免看起來覆雜,我把每個狀態分開了。雖然S1和S6狀態不存在,但是我還是畫出來方便理解。可以看到他們會自動跳轉到S0和S7。代碼中我也會列出方便理解。
module top_module (
input clk,
input reset,
input [3:1] s,
output fr3,
output fr2,
output fr1,
output dfr
);
parameter S0 = 4'b0000;
parameter S1 = 4'b0001;
parameter S2 = 4'b0010;
parameter S3 = 4'b0011;
parameter S4 = 4'b0110;
parameter S5 = 4'b0111;
parameter S6 = 4'b1110;
parameter S7 = 4'b1111;
reg [3:0] state,next_state;
always@(*)begin
case(state)
S0:next_state<= (s==7)?S0:(s>=3)?S3:(s>=1)?S5:S7;
S1:next_state<= (s==7)?S1:(s>=3)?S3:(s>=1)?S5:S7;
S2:next_state<= (s==7)?S0:(s>=3)?S2:(s>=1)?S5:S7;
S3:next_state<= (s==7)?S0:(s>=3)?S3:(s>=1)?S5:S7;
S4:next_state<= (s==7)?S0:(s>=3)?S2:(s>=1)?S4:S7;
S5:next_state<= (s==7)?S0:(s>=3)?S2:(s>=1)?S5:S7;
S6:next_state<= (s==7)?S0:(s>=3)?S2:(s>=1)?S4:S7;
S7:next_state<= (s==7)?S0:(s>=3)?S2:(s>=1)?S4:S7;
endcase
end
always@(posedge clk)begin
if(reset)begin
state <= S7;
end
else begin
state <= next_state;
end
end
assign {fr3,fr2,fr1,dfr} = state;
endmodule
另一參考
水位在S1下(S1,S2,S3=0):fr1,fr2,fr3,dfr=1;
水位在S2和S1之間(S1=1,S2,S3=0):fr1, fr2=1;
水位在S3和S2之間(S1,S2=1,S3=0):fr1=1;
水位超過S3(S1,S2,S3=1):fr1,fr2,fr3,dfr=0。
並要求前一時刻的水位高於當前時刻水位時(即放水過程)dfr=1。
本題中使用了6個狀態位,為直觀方便將轉換條件單獨提出。
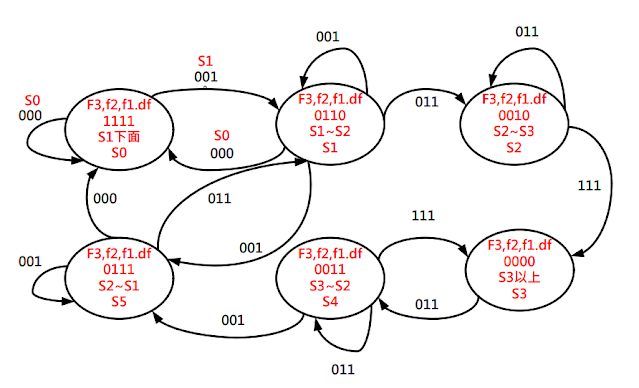
module top_module (
input clk,
input reset,
input [3:1] s,
output fr3,
output fr2,
output fr1,
output dfr
);
parameter S0 = 4'd0;
parameter S1 = 4'd1;
parameter S2 = 4'd2;
parameter S3 = 4'd3;
parameter S4 = 4'd4;
parameter S5 = 4'd5;
reg [2:0] state_c, state_n;
wire S02S1, S12S0, S12S2, S22S3, S22S5, S32S4, S42S5, S42S3, S52S0, S52S2;
always@(posedge clk) begin
if(reset)
state_c<=S0;
else
state_c <= state_n;
end
assign S02S1 = s[3:1] == 3'b001 && state_c == S0;
assign S12S0 = s[3:1] == 3'b000 && state_c == S1;
assign S12S2 = s[3:1] == 3'b011 && state_c == S1;
assign S22S3 = s[3:1] == 3'b111 && state_c == S2;
assign S22S5 = s[3:1] == 3'b001 && state_c == S2;
assign S32S4 = s[3:1] == 3'b011 && state_c == S3;
assign S42S5 = s[3:1] == 3'b001 && state_c == S4;
assign S42S3 = s[3:1] == 3'b111 && state_c == S4;
assign S52S0 = s[3:1] == 3'b000 && state_c == S5;
assign S52S2 = s[3:1] == 3'b011 && state_c == S5;
always@(*) begin
case(state_c)
S0:begin
if(S02S1)
state_n = S1;
else
state_n = state_c;
end
S1:begin
if(S12S2)
state_n = S2;
else if(S12S0)
state_n = S0;
else
state_n = state_c;
end
S2:begin
if(S22S3)
state_n = S3;
else if(S22S5)
state_n = S5;
else
state_n = state_c;
end
S3:begin
if(S32S4)
state_n = S4;
else
state_n = state_c;
end
S4:begin
if(S42S5)
state_n = S5;
else if(S42S3)
state_n = S3;
else
state_n = state_c;
end
S5:begin
if(S52S0)
state_n = S0;
else if(S52S2)
state_n = S2;
else
state_n = state_c;
end
endcase
end
// Output logic
// assign out = (state == ...);
assign fr3 = state_c == S0;
assign fr2 = state_c == S0 || state_c == S1 || state_c == S5;
assign fr1 = state_c == S0 || state_c == S1 || state_c == S2 || state_c==S4 || state_c==S5;
assign dfr = state_c == S0 || state_c == S4 || state_c == S5;
endmodule
另一參考
module top_module (
input clk,
input reset,
input [3:1] s,
output reg fr3,
output reg fr2,
output reg fr1,
output reg dfr
);
parameter A2=0, B1=1, B2=2, C1=3, C2=4, D1=5;
reg [2:0] state, next; // Make sure these are big enough to hold the state encodings.
// Edge-triggered always block (DFFs) for state flip-flops. Synchronous reset.
always @(posedge clk) begin
if (reset)
state <= A2;
else
state <= next;
end
// what should be next state be?
// Combinational always block: Use blocking assignments.
always@(*) begin
case (state)
A2: next = s[1] ? B1 : A2;
B1: next = s[2] ? C1 : (s[1] ? B1 : A2);
B2: next = s[2] ? C1 : (s[1] ? B2 : A2);
C1: next = s[3] ? D1 : (s[2] ? C1 : B2);
C2: next = s[3] ? D1 : (s[2] ? C2 : B2);
D1: next = s[3] ? D1 : C2;
default: next = 'x;
endcase
end
always@(*) begin
case (state)
A2: {fr3, fr2, fr1, dfr} = 4'b1111;
B1: {fr3, fr2, fr1, dfr} = 4'b0110;
B2: {fr3, fr2, fr1, dfr} = 4'b0111;
C1: {fr3, fr2, fr1, dfr} = 4'b0010;
C2: {fr3, fr2, fr1, dfr} = 4'b0011;
D1: {fr3, fr2, fr1, dfr} = 4'b0000;
default: {fr3, fr2, fr1, dfr} = 'x;
endcase
end
endmodule