C語言 例題5-6 四階 Runge-Kutta 解 ODE y'= -y + t^2 + 1 , 0<=t<=1 , y(0)=1 , 真實解 W(t)= -2e^(-t) + t ^2 - 2t + 3
//Code for RUNGE-KUTTA 4th ORDER METHOD in C Programming
// dy/dx = -y +x^2 +1 , 0<= x <=1 , y(0)=1
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double rk4(double(*f)(double, double), double dx, double x, double y)
{
double k1 = dx * f(x, y),
k2 = dx * f(x + dx / 2, y + k1 / 2),
k3 = dx * f(x + dx / 2, y + k2 / 2),
k4 = dx * f(x + dx, y + k3);
return y + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
}
double rate(double x, double y)
{
return (-y+ (x*x) +1);
}
int main(void)
{
double *y, x, y2;
double x0 = 0, x1 = 1, dx = .001;
int i, n = 1 + (x1 - x0)/dx;
y = (double *)malloc(sizeof(double) * n);
for (y[0] = 1, i = 1; i < n; i++)
y[i] = rk4(rate, dx, x0 + dx * (i - 1), y[i-1]);
printf(" x\t y\t real. err.\n------------------------------------------\n");
for (i = 0; i < n; i++)
{
x = x0 + dx * i;
y2 = -2*exp(-x) + pow(x, 2) -2*x +3;
if (i%100==0)
printf("%0.2lf\t%0.7lf\t%0.7lf\t%0.7lf\n", x, y[i], y2, (y[i]/y2 - 1));
}
return 0;
}
輸出畫面
x y real. err.
------------------------------------------
0.00 1.0000000 1.0000000 0.0000000
0.10 1.0003252 1.0003252 0.0000000
0.20 1.0025385 1.0025385 0.0000000
0.30 1.0083636 1.0083636 0.0000000
0.40 1.0193599 1.0193599 0.0000000
0.50 1.0369387 1.0369387 0.0000000
0.60 1.0623767 1.0623767 0.0000000
0.70 1.0968294 1.0968294 0.0000000
0.80 1.1413421 1.1413421 0.0000000
0.90 1.1968607 1.1968607 0.0000000
1.00 1.2642411 1.2642411 0.0000000
訂閱:
張貼留言 (Atom)
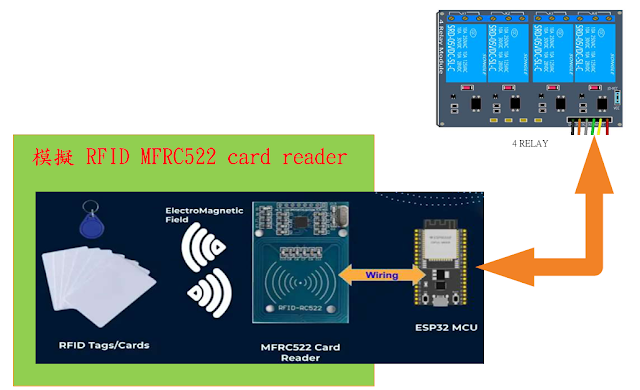
WOKWI 模擬RFID UID產生 暨 4LED on,off,flash控制(1)
WOKWI 模擬RFID UID產生 暨 4LED on,off,flash控制(1) #include < ArduinoMqttClient.h > #include < WiFi.h > //MFRC522 程式庫 模擬mfrc522 送出卡號...
-
python pip 不是内部或外部命令 -- 解決方法 要安裝 Pyqt5 1. 首先,開啟命令提示字元。 2. 輸入 pip3 install pyqt5 好像不能執行 ! ! 錯誤顯示 : ‘ pip3 ’ 不是內部或外部命令、可執行的程式或批...
-
課程講義 下載 11/20 1) PPT 下載 + 程式下載 http://www.mediafire.com/file/cru4py7e8pptfda/106%E5%8B%A4%E7%9B%8A2-1.rar 11/27 2) PPT 下載...
-
• 認 識 PreFix、InFix、PostFix PreFix(前序式):* + 1 2 + 3 4 InFix(中序式): (1+2)*(3+4) PostFix(後序式):1 2 + 3 4 + * 後 序式的運算 例如: 運算時由 後序式的...

沒有留言:
張貼留言