'''
例題 6-1 利用高斯消去法 求 n x n 線性代數的解
/* ex6-1.c based on Gaussian Elimination method
* for solving the n x n linear algebra system
* a11 x1+a12 x2+...+a1n xn=b1
* a21 x1+a22 x2+...+a2n xn=b2
* . . . .
* . . . .
* an1 x1+an2 x2+...+ann xn=bn
* Input number of unknowns and equations n
* with coefficent a11,a12,...,ann and b1,b2,
* ...bn. Output solution x1,x2,x3,...,xn.
*/
'''
def myGauss(m):
#eliminate columns
for col in range(len(m[0])):
for row in range(col+1, len(m)):
r = [(rowValue * (-(m[row][col] / m[col][col]))) for rowValue in m[col]]
m[row] = [sum(pair) for pair in zip(m[row], r)]
#now backsolve by substitution
ans = []
m.reverse() #makes it easier to backsolve
for sol in range(len(m)):
if sol == 0:
ans.append(m[sol][-1] / m[sol][-2])
else:
inner = 0
#substitute in all known coefficients
for x in range(sol):
inner += (ans[x]*m[sol][-2-x])
#the equation is now reduced to ax + b = c form
#solve with (c - b) / a
ans.append((m[sol][-1]-inner)/m[sol][-sol-2])
ans.reverse()
return ans
#=======================
a1=[[-3.0,2.0,-6.0,6.0],
[5.0,7.0,-5.0,6.0],
[1.0,4.0,-2.0,8.0]]
a= myGauss(a1)
n=3
for i in range(0 ,n):
for j in range(0,n+1):
print( "a[",i,"][",j,"]=",round(a1[i][j],4),'\t',end='')
print("")
print("x1=",round(a[0],4), '\t',"x2=",round(a[1],4), '\t',"x3=",round(a[2],4) )
print()
#=======================
a1=[[-1.0 , 1.0 , 2.0 , 2.0],
[3.0 , -1.0 , 1.0 , 6.0],
[-1.0 , 3.0 , 4.0 , 4.0]]
a= myGauss(a1)
n=3
for i in range(0 ,n):
for j in range(0,n+1):
print( "a[",i,"][",j,"]=",round(a1[i][j],4),'\t',end='')
print("")
print("x1=",round(a[0],4), '\t',"x2=",round(a[1],4), '\t',"x3=",round(a[2],4) )
print()
#=======================
a1=[[2.0 , -1.5 , 3.0 , 1.0] ,
[-1.0 , 0.0 , 2.0 , 3.0] ,
[ 4.0 ,-4.5 , 5.0 , 1.0] ]
n=3
a= myGauss(a1 )
for i in range(0 ,n):
for j in range(0,n+1):
print( "a[",i,"][",j,"]=",round(a1[i][j],4),'\t',end='')
print("")
print("x1=",round(a[0],4), '\t',"x2=",round(a[1],4), '\t',"x3=",round(a[2],4) )
print()
#=======================
a1=[[4.01 , 1.23 , 1.43 , -0.73 , 5.94],
[1.23 , 7.41 , 2.41 , 3.02 , 14.07],
[1.43 , 2.41 , 5.79 , -1.11 , 8.52],
[-0.73 , 3.02 , -1.11 , 6.41 , 7.59]]
n=4
a= myGauss(a1)
for i in range(0 ,n):
for j in range(0,n+1):
print( "a[",i,"][",j,"]=",round(a1[i][j],4),'\t',end='')
print("")
print("x1=",round(a[0],4), '\t',"x2=",round(a[1],4), '\t',"x3=",round(a[2],4), '\t',"x4=",round(a[3],4) )
#=======================
======== RESTART: F:\2018-09勤益科大數值分析\數值分析\PYTHON\EX6-1-1.py ===========
a[ 0 ][ 0 ]= 0.0 a[ 0 ][ 1 ]= 0.0 a[ 0 ][ 2 ]= 2.7742 a[ 0 ][ 3 ]= 2.7742
a[ 1 ][ 0 ]= 0.0 a[ 1 ][ 1 ]= 10.3333 a[ 1 ][ 2 ]= -15.0 a[ 1 ][ 3 ]= 16.0
a[ 2 ][ 0 ]= -3.0 a[ 2 ][ 1 ]= 2.0 a[ 2 ][ 2 ]= -6.0 a[ 2 ][ 3 ]= 6.0
x1= -2.0 x2= 3.0 x3= 1.0
a[ 0 ][ 0 ]= 0.0 a[ 0 ][ 1 ]= 0.0 a[ 0 ][ 2 ]= -5.0 a[ 0 ][ 3 ]= -10.0
a[ 1 ][ 0 ]= 0.0 a[ 1 ][ 1 ]= 2.0 a[ 1 ][ 2 ]= 7.0 a[ 1 ][ 3 ]= 12.0
a[ 2 ][ 0 ]= -1.0 a[ 2 ][ 1 ]= 1.0 a[ 2 ][ 2 ]= 2.0 a[ 2 ][ 3 ]= 2.0
x1= 1.0 x2= -1.0 x3= 2.0
a[ 0 ][ 0 ]= 0.0 a[ 0 ][ 1 ]= 0.0 a[ 0 ][ 2 ]= -8.0 a[ 0 ][ 3 ]= -8.0
a[ 1 ][ 0 ]= 0.0 a[ 1 ][ 1 ]= -0.75 a[ 1 ][ 2 ]= 3.5 a[ 1 ][ 3 ]= 3.5
a[ 2 ][ 0 ]= 2.0 a[ 2 ][ 1 ]= -1.5 a[ 2 ][ 2 ]= 3.0 a[ 2 ][ 3 ]= 1.0
x1= -1.0 x2= -0.0 x3= 1.0
a[ 0 ][ 0 ]= 0.0 a[ 0 ][ 1 ]= 0.0 a[ 0 ][ 2 ]= 0.0 a[ 0 ][ 3 ]= 4.1263 a[ 0 ][ 4 ]= 4.1263
a[ 1 ][ 0 ]= 0.0 a[ 1 ][ 1 ]= 0.0 a[ 1 ][ 2 ]= 4.7274 a[ 1 ][ 3 ]= -1.759 a[ 1 ][ 4 ]= 2.9685
a[ 2 ][ 0 ]= 0.0 a[ 2 ][ 1 ]= 7.0327 a[ 2 ][ 2 ]= 1.9714 a[ 2 ][ 3 ]= 3.2439 a[ 2 ][ 4 ]= 12.248
a[ 3 ][ 0 ]= 4.01 a[ 3 ][ 1 ]= 1.23 a[ 3 ][ 2 ]= 1.43 a[ 3 ][ 3 ]= -0.73 a[ 3 ][ 4 ]= 5.94
x1= 1.0 x2= 1.0 x3= 1.0 x4= 1.0
>>>
訂閱:
張貼留言 (Atom)
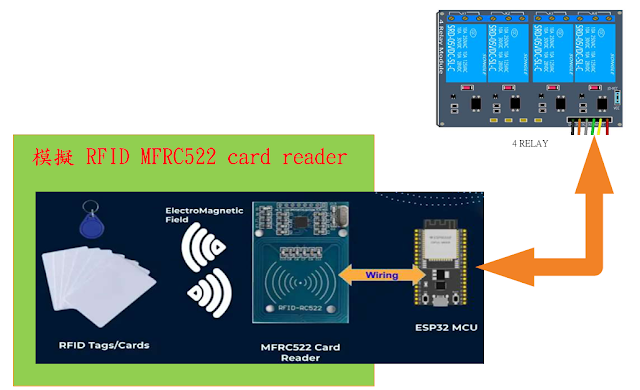
WOKWI 模擬RFID UID產生 暨 4LED on,off,flash控制(1)
WOKWI 模擬RFID UID產生 暨 4LED on,off,flash控制(1) #include < ArduinoMqttClient.h > #include < WiFi.h > //MFRC522 程式庫 模擬mfrc522 送出卡號...
-
python pip 不是内部或外部命令 -- 解決方法 要安裝 Pyqt5 1. 首先,開啟命令提示字元。 2. 輸入 pip3 install pyqt5 好像不能執行 ! ! 錯誤顯示 : ‘ pip3 ’ 不是內部或外部命令、可執行的程式或批...
-
課程講義 下載 11/20 1) PPT 下載 + 程式下載 http://www.mediafire.com/file/cru4py7e8pptfda/106%E5%8B%A4%E7%9B%8A2-1.rar 11/27 2) PPT 下載...
-
• 認 識 PreFix、InFix、PostFix PreFix(前序式):* + 1 2 + 3 4 InFix(中序式): (1+2)*(3+4) PostFix(後序式):1 2 + 3 4 + * 後 序式的運算 例如: 運算時由 後序式的...

沒有留言:
張貼留言